1、给出下列几个命题：
①至少有一个x0，使x02＋2x0＋1＝0成立；
②对任意的x，都有x2＋2x＋1＝0成立；
③对任意的x，都有x2＋2x＋1＝0不成立；
④存在x0，使x02＋2x0＋1＝0成立．
其中是全称命题的个数为（ ）
A．1 B．2
C．3 D．0
2、将“x2＋y2≥2xy”改写成全称命题，下列说法正确的是（ ）
A．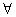
x，y∈R，都有x2＋y2≥2xy
B．
x0，y0∈R，使x02＋y02≥2x0y0
C．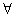
x>0，y>0，都有x2＋y2≥2xy
D．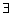
x0<0，y0<0，使x02＋y02≤2x0y0
3、命题“存在x∈Z使x2＋2x＋m≤0”的否定是（ ）
A．存在x∈Z使x2＋2x＋m>0
B．不存在x∈Z使x2＋2x＋m>0
C．对任意x∈Z使x2＋2x＋m≤0
D．对任意x∈Z使x2＋2x＋m>0
4、已知命题p：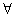
x∈R，sinx≤1，则（ ）
A．非p：
x∈R，sinx≥1
B．非p：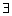
x0∈R，sinx0≥1
C．非p：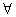
x∈R，sinx>1
D．非p：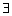
x0∈R，sinx0>1
5、已知命题p：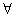
x∈R，2x2＋2x＋
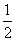<0；命题q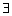：x∈R，sinx－cosx＝
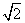．则下列判断正确的是（ ）
A．p是真命题 B．q是假命题
C．非p是假命题 D．非q是假命题
6、填上适当的量词符号“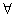
”“
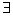”，使下列命题为真命题．
(1)_________x∈R，使x2＋2x＋1≥0；
(2) _________α，β∈R，使cos(α－β)＝cosα－cosβ；
(3) _________a，b∈R，使方程组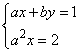
有唯一解．
7、给出下列4个命题：
①
；
②矩形都不是梯形；
③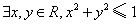
；
④任意互相垂直的两条直线的斜率之积等于－1．
其中全称命题是_________．
8、以下三个命题：
①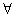
α∈R，在[α，α＋π]上函数y＝sinx都能取到最大值1；
②若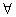
a∈R，且a≠0，f(x＋a)＝－f(x)对
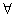x∈R成立，则f(x)为周期函数；
③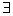
x∈(－
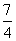π，－
π)，使sinx<cosx．其中正确命题为__________．
x∈R，使得x
x∈R，r(x)与s(x)有且仅有一个是真命题，求实数m的取值范围．
