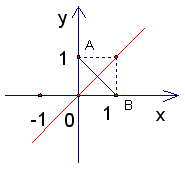| 曲线与方程 |
主编:黄冈中学数学集体备课组
思考:
(1)以
为圆心,r为半径的圆的方程是
,请探讨一下圆上的点的坐标与方程的解的关系.
答案:
圆上任意一点
的坐标都符合方程,即有
;反之,若某点
符合
,则此点
一定在圆上.
(2)求如图所示的AB的垂直平分线
的方程.
答案:
易知AB垂直平分线过原点,斜率为1,所以AB的垂直平分线的方程为
.AB的垂直平分线上任意一点
的坐标都符合方程
,反之符合方程
的解
构成的点都在AB的垂直平分线上.
(3)下列方程能表示(2)中的直线吗?为什么?
①
;②
;③|x|-y=0
答案:
①中,曲线C上的点不全都是方程
的解,如点(-1,-1)等,即不符合“曲线上的点的坐标都是方程的解”这一结论;
②中,尽管“曲线C上的坐标都是方程的解”,但以方程
的解为坐标的点不全在曲线C上,如点(2,-2)等,即不符合“以方程的解为坐标的点都在曲线上”这一结论;
③中,类似①②得出不符合“曲线上的点的坐标都是方程的解”,“以方程的解为坐标的点都在曲线上”.
所以我们要方程是曲线的方程,曲线是表示方程的曲线,可以给出如下的定义:
1、“曲线的方程”和“方程的曲线”
在直角坐标系中,如果某曲线C上的点与一个二元方程的实数解建立了如下关系:
(1)曲线上的点的坐标都是这个方程的解;(纯粹性)
(2)以这个方程的解为坐标的点都是曲线上的点.(完备性)
那么,这个方程叫做曲线的方程;这条曲线叫做方程的曲线.
说明:(1)曲线的方程:反映的是图形所满足的数量关系;方程的曲线:反映的是数量关系所表示的图形.
(2)两者的关系:点在曲线上
点的坐标适合此曲线的方程,即曲线上所有的点的集合与曲线方程的解集能够一一对应.
(3)如果曲线C的方程是
,那么点
在曲线上的充要条件是
.
例1、解答下列问题,且说出各依据了曲线的方程和方程的曲线定义中的哪一个关系?
(1)点
是否在方程为
的圆上?
(2)已知方程为
的圆过点
,求m的值.
答案:
(1)依据关系(2),可知点
在圆上,
不在圆上,用到以这个方程的解为坐标的点都是曲线上的点.
(2)依据关系(1),求得
,用到曲线上的点的坐标都是这个方程的解.
例2、(1)举出一个方程与曲线,使它们之间的关系符合条件①而不符合条件②;
(2)举出一个方程与曲线,使它们之间的关系符合条件②而不符合条件①.
(3)举出一个方程与曲线,使它们之间的关系既符合条件②也符合条件①.
答案:
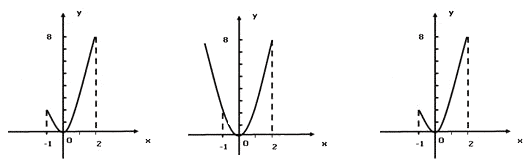
(1)方程
,曲线如上图左,符合条件①而不符合条件②;
(2)方程
(
),曲线如上图中,符合条件②而不符合条件①;
(3)方程
(
),曲线如上图右,符合条件②也符合条件①.
例3、点M到两条互相垂直的直线的距离相等,求点M的轨迹方程.
解:
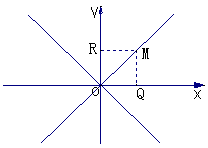
取已知两条互相垂直的直线为坐标轴,建立直角坐标系,如图所示,设点M的坐标为
,点M的轨迹就是到坐标轴的距离相等的点的集合P={M||MR|=|MQ|},其中Q、R分别是点M到x轴、y轴的垂线的垂足.
因为点M到x轴、y轴的距离分别是它的纵坐标和横坐标的绝对值,所以条件|MR|=|MQ|可写成|
|=|
|即
±
=0 ①
下面证明①式是所求轨迹的方程
(1)由求方程的过程可知,曲线上的点的坐标都是方程①的解;
(2)设点
的坐标
是方程①的解,那么x1±y1=0,即|x1|=|y1|,而|x1|、|y1|正是点
到纵轴、横轴的距离,因此点
到这两条直线的距离相等,点是曲线上的点.
由(1)(2)可知,方程①是所求轨迹的方程,图形如图所示.
2、求简单的曲线方程的一般步骤:
(1)建立适当的坐标系,用有序实数对表示曲线上任意一点M的坐标;
(2)写出适合条件P的点M的集合;
(3)用坐标表示条件P(M),列出方程;
(4)化方程为最简形式;
(5)证明以化简后的方程的解为坐标的点都是曲线上的点.
一般的,化简前后的方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可以适当说明.另外可以根据情况省略步骤(2),直接列出曲线方程.
例4、已知一曲线是与两个定点
、
距离的比为
的点的轨迹,求曲线的方程.
解:
在给定的坐标系里,设
是曲线上的任意一点,点M属于集合
,
代入坐标得
,
化简得
,即为所求的曲线方程.
3、求轨迹方程的常见方法:
(1)直接法:通过建立适当的坐标系,设点、列式、化简从而得出轨迹方程.如例4就是直接法的应用.
(2)几何法:指利用平面几何或解析几何知识分析图形性质,发现动点的运动规律和要满足的条件,从而得到动点的轨迹方程.
例5、已知点
、
,过
、
作两条互相垂直的直线
和
,求
和
的交点
的轨迹方程.
解:
由平面几何知识可知,当
为直角三角形时,点
的轨迹是以
为直径的圆,此圆的圆心即为
的中点
,半径为
(备注:老师讲解时出现口误,应该是
),方程为
.
故
的轨迹方程为
.
(3)相关点法:当题目中有多个动点时,将其他动点(备注:视频中删除此处的P)的坐标用所求动点P(备注:视频中加上P)的坐标来表示,再代入到其他动点要满足的条件或轨迹方程中,整理即得到动点P的轨迹方程,称之代入法,也称相关点法、转移法.
例6、已知△ABC的顶点
,顶点
在抛物线
上运动,求
的重心
的轨迹方程.
解:
设
,
.
又G为△ABC的重心,
∴有3y=(3x+2)2(备注:视频中x0改为x)
.
又A、B、C要构成三角形,则
.
∴所求的轨迹方程为
.
(4)交轨法:利用两个轨迹的交点建立等式,消去参数得到所求方程.
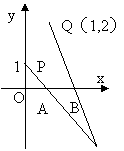
例7、如图,长度为1的线段AB在x轴上移动,点P(0,1)与A点连成直线PA,点Q(1,2)与B点连成直线QB,求直线PA与直线QB交点的轨迹方程.
解:
如图,设PA与QB的交点为M(x,y),A(a,0),则B(a+1,0).
由截距式方程,得PA的方程为
,即x+ay=a.
由两点式方程,得QB的方程为
,即2x+ay-2a-2=0(a≠0).
两直线的交点就是M,故M是
的解,
消去参数a,得M的轨迹方程为(2-x)y=2(x≠0).
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -