提示:
1、条件中曲线C上的点的坐标(x,y)都是方程F(x,y)=0的解,满足了曲线和方程的概念的条件(1),而且阐明曲线C上没有坐标不满足方程F(x,y)=0的点,也就是说,坐标不满足F(x,y)=0的点不在曲线C上.故选D.由条件无法判定满足曲线和方程的概念的条件(2),从而选项A、B、C是错误的.
2、由对数的真数大于0,得x+2y>0,∴A(0,-3)、C( )不合要求;将B(0,4)代入方程检验,不合要求;将D(4,0)代入方程检验,合乎要求.故选B. )不合要求;将B(0,4)代入方程检验,不合要求;将D(4,0)代入方程检验,合乎要求.故选B.
3、方程|x|=2的一组解(-2,1)显然不在l上,A错;轨迹上的点(-1,1)不满足方程y=x,B错;单位圆上存在点(0,-1)不满足方程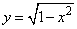 ,C错;由以上可排除A、B、C,选D. ,C错;由以上可排除A、B、C,选D.
4、方程可变为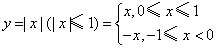 . .
5、y=|x|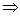 |y|=|x|成立,但逆推不成立. |y|=|x|成立,但逆推不成立.
6、∵x2+xy=x,∴x2+xy-x=0即x(x+y-1)=0,即x=0或x+y-1=0表示两条直线. |