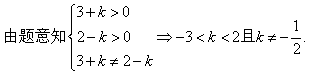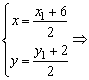| 椭圆及其标准方程 |
主编:黄冈中学数学集体备课组
动画见视频(备注:视频中数据有些小问题,但不影响椭圆性质的研究)
1、椭圆的定义:
平面内到两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.定点F1、F2称为椭圆的焦点.F1、F2间的距离|F1F2|称为焦距.
注意问题:(1)平面内是一个大前提,不可少;
(2)距离之和这个常数要大于两个定点间的距离.
2、标准方程的推导
由椭圆的定义,可以知道它的基本几何特征,但对椭圆还具有哪些性质,我们还一无所知,所以需要用坐标法先建立椭圆的方程.如何建立椭圆的方程?根据求曲线方程的一般步骤,可分:(1)建系设点;(2)点的集合;(3)代数方程;(4)化简方程等步骤.
推导过程:
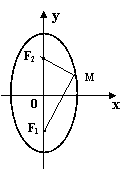
以过F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系.
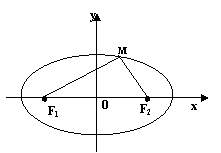
设M(x,y)是椭圆上任意一点,椭圆的焦距|F1F2|为2c(c>0)、正常数为2a,则F1(-c,0)、F2(c,0).
根据椭圆的定义可得
的集合:
,
代入点的坐标得
,
,
两边平方整理得:
,
再次平方得
,
两边同时除以
得:
,
如果建立平面直角坐标系时,椭圆的焦点坐标在
轴上,焦点为
,则同上可求得椭圆方程为
.
由椭圆的定义可知,
,
,进而引进
,此时
,从而得到
.
椭圆的标准方程:
焦点在x轴:
,焦点F1(-c,0)、F2(c,0).
焦点在y轴:
,焦点 F1(0,-c)、F2(0,c).
例1、下列方程是否表示椭圆,如果是,判断它的焦点在哪个坐标轴上?并写出
、
的值及焦点坐标.
;
;
;
.
解:
(1)焦点在
轴上,
,
,焦点坐标为
;
(2)方程化为
,不是椭圆的标准方程;
(3)方程化为
,焦点在y轴上,
,
,焦点坐标为
;
(4)
,∴焦点在y轴上,∴
,
,焦点坐标为
.
例2、求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(0,-2)、(0,2),并且椭圆经过点
;
解:
椭圆的焦点在y轴上,设椭圆方程为
.
.
∴椭圆的标准方程为
.
(2)两个焦点的距离为8,椭圆上一点P到两焦点的距离和等于10;
解:
由题意知:2c=8,2a=10,∴a=5,c=4,∴b2=25-16=9.
当焦点在x轴上时,椭圆的方程为
.
当焦点在y轴上时,椭圆的方程为
.
(3)中心在原点,焦点在坐标轴上,且经过两点
、
;
解:
设椭圆的方程为
(
且
),
代入点
的坐标得
解得:
,
所以椭圆的标准方程为
.
(4)经过点(2,-3)且与椭圆
具有共同的焦点.
解:
椭圆
化为标准方程为
,
其焦点坐标为
,
设椭圆的标准方程为:
(
),代入点(2,-3)得
,
解得
或
(舍),所以得到椭圆的标准方程为
.
例3、若方程
表示椭圆,则k的取值范围为__________.
解:
答案:
.
例4、设定点A(6,2),P是椭圆
上动点,求线段AP中点M的轨迹方程.
解:
设M(x,y),
.
∵
为线段
的中点,∴
,
又
在椭圆上,
,
∴点
的轨迹方程为
.
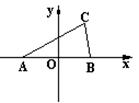
例5、如图,设△
的两个顶点
,B(a,0),顶点C在移动,且
,且k<0,试求动点C的轨迹方程.
解:
设点C(x,y),则
,
,
又
,
,
化简即可得点M的轨迹方程为
(
).
例6、已知△ABC中,A(3,0),B(-3,0),三边AC、AB、BC的长成等差数列,求顶点C的轨迹方程.
解:
设C(x,y),由题设|AB|=6,∵AC、AB、BC三边成等差数列,
∴|AC|+|BC|=2|AB|=12>|AB|.
根据椭圆定义,点C的轨迹是以A、B为焦点的椭圆,且2c=6,2a=12,∴c=3,a=6,b2=27.
∴顶点C的轨迹方程是
.注意椭圆与x轴的交点与A、B不能构成三角形,故顶点C的轨迹方程是
.
年级 |
课程名称 |
免费听课 |
课程详情 |
| 高一全科点睛班课程 |
|||
| 高一全科强化班课程 | |||
| 高二全科全年强化班 |
|||
| 高三全科强化班课程 |
|||
| 初一全科强化班课程 | |||
| 初一全科点睛班课程 | |||
| 初二全科强化班视频 |
|||
| 初二全科点睛班课程 |
|||
| 初三全科强化班 |
|||
| 全科巨无霸同步提高课程 | |||
| 小学全年全科强化班 |
|||
- 返回 -