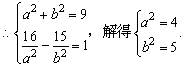| 双曲线及其标准方程 |
主编:黄冈中学数学集体备课组
1、双曲线的定义:平面内到两定点F1,F2的距离的差的绝对值为常数(小于|F1F2|)的动点的轨迹叫双曲线,即
.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距,记为2c.
说明:(1)“平面内”是大前提;
(2)“距离的差的绝对值”不可少,没有“绝对值”则只能表示双曲线的一支;
(3)“常数小于|F1F2|”,若大于|F1F2|则点的轨迹不存在;若等于|F1F2|则轨迹为两条射线.
2、双曲线的标准方程:
根据双曲线的定义推导双曲线的标准方程:推导标准方程的过程就是求曲线方程的过程,可根据求动点轨迹方程的步骤,求出双曲线的标准方程.过程如下:(1)建系设点;(2)点的集合;(3)代数方程;(4)化简方程等步骤.
取过焦点F1,F2的直线为x轴,线段F1F2的垂直平分线为y轴.设M(x,y)为双曲线上的任意一点,双曲线的焦距是2c(c>0),则
,又设M与
距离之差的绝对值等于2a(常数),2a<2c.
,
,
化简,得:
.
由定义
,
.
令
代入得:
.
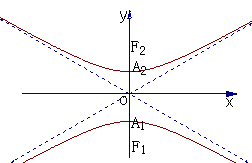
若坐标系的选取不同,焦点在y轴上,则焦点是
,同理得到
.
双曲线的标准方程为:
(1)
,焦点在x轴上,焦点是
;
(2)
,焦点在y轴上,焦点是
.
在两个标准方程中都有
,且
,a与b的大小关系可以为
.
例1、判断下列方程是否表示双曲线,若是,求出三量a,b,c的值.
①
答案:是双曲线,
;
②
答案:是双曲线,
;
③
答案:是双曲线,
;
④
答案:是双曲线,当m>0时,
;当m<0时,
.
例2、已知双曲线两个焦点的坐标为
,双曲线上一点P到
的距离之差的绝对值等于6,求双曲线标准方程.
解:
由题可设双曲线方程为:
(
,
).
易知:c=5,2a=6,∴a=3,
,
∴双曲线的标准方程为
.
变式1:已知两定点
,平面上一动点P,满足
,求点P的轨迹方程.
解:
由题意知:P点的轨迹是双曲线的右支,同上求得双曲线的方程为
,所以P点的轨迹方程是
.
变式2:已知两定点
,平面上一动点P,满足
,求点P的轨迹方程.
解:
因为
,所以点P的轨迹是分别以F1,F2为端点的两条射线,其轨迹方程是:y=0(x≤-5或x≥5)
变式3:已知双曲线的焦距为10,双曲线上一点P到两焦点F1,F2的距离的差的绝对值等于6,求双曲线的标准方程.
解:
由题意知:2c=10,2a=6,∴c=5,a=3,∴b=4.
∴当焦点在x轴上时,方程为
.
当焦点在y轴上时,方程为
.
例3、判断方程
所表示的曲线.
解:
①当
时,即当3<k<9时,是双曲线.
②当
时,即当k<3(备注:视频中将x改成k)时,是椭圆.
例4、求适合下列条件的双曲线的标准方程:
,经过点(-5,2),焦点在x轴上;
解:设双曲线的方程为
.
由题意知
.
∴所求双曲线的方程为
.
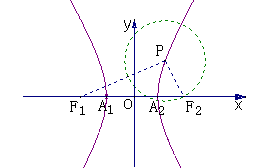
例5、设双曲线与椭圆
有共同的焦点,且与椭圆相交,在第一象限的交点A的纵坐标为4,求此双曲线的方程.
解:
椭圆
的焦点为(0,-3)、(0,3).
当A的纵坐标为4时,
.
设双曲线的方程为
.
∴双曲线的方程为
.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -