直线与双曲线位置关系问题
求解的基本策略是,将其转化为直线与双曲线方程的方程组的解的问题,进而转化为一元二次方程的实根问题,因而判别式、韦达定理、弦长公式、焦半径公式的应用,以及设而不求、整体代入、数形结合的思想方法技巧在这里起着极为重要的作用.
例、直线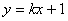 与双曲线
与双曲线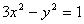 相交于不同两点A、B.
相交于不同两点A、B.
(1)以AB为直径的圆恰好过原点,求k的值.
(2)是否存在k,使A、B两点关于直线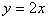 对称?若存在,求出k值;若不存在,请说明理由.
对称?若存在,求出k值;若不存在,请说明理由.
分析:
(1)所给圆过原点的条件为 (C为AB中点),将其转化为k的方程;(2)用假设法求解.
(C为AB中点),将其转化为k的方程;(2)用假设法求解.
解:
(1)将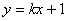 代入
代入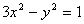 ,消去y,得:
,消去y,得: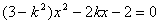
依题意知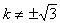 ,由
,由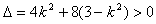 ,
,
得 或
或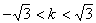 或
或
设A(x1,y1),B(x2,y2),AB中点C(x0,y0),由韦达定理,
得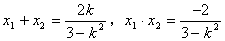
于是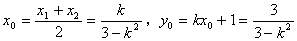
即C(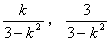 )
)
因以AB为直径的圆过原点,则在Rt△AOB中, ,由两点距离公式及弦长公式,得:
,由两点距离公式及弦长公式,得:
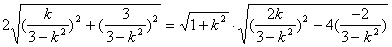
化简,得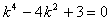 ,解得
,解得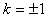 或
或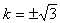 (舍去)
(舍去)
(2)假设存在k,使A、B关于直线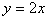 对称,则直线
对称,则直线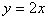 垂直平分线段AB,于是
垂直平分线段AB,于是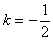 且AB中点在直线
且AB中点在直线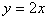 上.
上.
由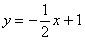 与
与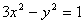 联立,消去y,得:
联立,消去y,得: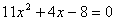
由韦达定理、中点公式,可得AB中点C(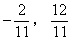 )
)
显然点C不在直线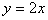 上,故满足条件的k不存在.
上,故满足条件的k不存在.
评注:
(1)中要注意双曲线与直线方程联立得到相应的一元二次方程的二次项系数,对它们交点个数的影响;(2)属探索型问题,也是高考中的常见题型,基本解法有假设法、反证法.