例1、(辽宁卷)设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A.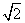 B.
B.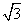 C.
C.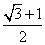 D.
D.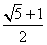
解析:
不妨设双曲线的焦点在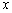 轴上,设其方程为
轴上,设其方程为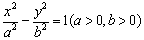 ,
,
则一个焦点为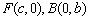 .
.
一条渐近线斜率为 ,直线
,直线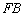 的斜率为
的斜率为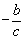 ,
,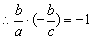 ,
,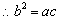 .
.
∴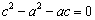 ,∴e2-e-1=0,解得
,∴e2-e-1=0,解得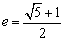 .
.
答案:D
例2、(上海卷)已知双曲线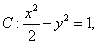 设过点
设过点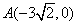 的直线l的方向向量
的直线l的方向向量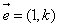 .
.
(1)当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2)证明:当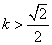 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为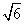 .
.
解析:
(1)双曲线C的渐近线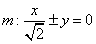 ,
,
∴直线l的方程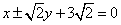 ,
,
直线l与m的距离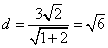 .
.
(2)设过原点且平行于l的直线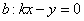 .
.
则直线l与b的距离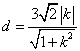 .
.
当 .
.
又双曲线C的渐近线为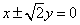 .
.
∴双曲线C的右支在直线b的右下方,
故在双曲线C的右支上不存在点Q,使之到直线l的距离为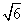 .
.