| 双曲线的简单几何性质 |
主编:黄冈中学数学集体备课组
双曲线的标准方程为:
(1)
,焦点在x轴上,焦点是
;
(2)
,焦点在y轴上,焦点是
.
在两个标准方程中都有
,且
;
a,b,c中c最大,a,b的大小关系没有要求.
类比椭圆的研究方法,我们可以根据双曲线的标准方程
(
),来研究双曲线的性质.
1、范围
由双曲线的标准方程得:
,进一步得:
,或
.这说明双曲线在不等式
,或
所表示的区域;而y的取值可以是所有实数.
2、对称性
把方程中的x换成-x方程不变,图象关于y轴对称.
把方程中的y换成-y方程不变,图象关于x轴对称.
把x,y同时换成-x,-y方程也不变,图象关于原点对称.
原点叫双曲线的对称中心,简称中心.x轴、y轴叫双曲线的对称轴.即双曲线既是轴对称图形,又是中心对称图形.
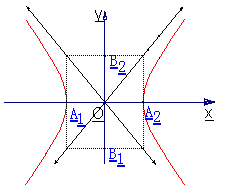
3、顶点
圆锥曲线的顶点的统一定义,即圆锥曲线的对称轴与圆锥曲线的交点叫做圆锥曲线的顶点.
在双曲线的方程里,令
,得
,因此双曲线和x轴有两个交点
,即为双曲线的两个顶点;
在双曲线的方程里,令
,得
,这个方程没有实数根,即双曲线和y轴没有交点,但我们还是把
画在y轴上;
线段A1A2叫做双曲线的实轴,它的长等于2a,a叫做双曲线的半实轴长;线段B1B2叫做双曲线的虚轴,它的长等于2b,b叫做双曲线的半虚轴长.
4、渐近线
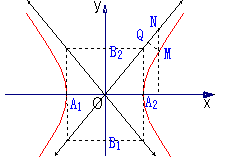
直线
叫做双曲线
的渐近线;
=
(
).
渐进线的求法:解
即得.
等轴双曲线:渐近线为
的双曲线,即a=b的双曲线.
5、离心率
双曲线的焦距与实轴长的比
叫做双曲线的离心率(
).
双曲线形状与e的关系:
,
因此e越大,即渐近线的斜率的绝对值就大,这时双曲线的形状就从狭窄逐渐变得开阔.由此可知,双曲线的离心率越大,它的开口就越阔.
例1、图中共顶点的椭圆①、②与双曲线③、④的离心率分别为e1、e2、e3、e4,其大小关系为( )
A.e1<e2<e3<e4 B.e2<e1<e3<e4
C.e1<e2<e4<e3 D.e2<e1<e4<e3
解:
易知e1,e2∈(0,1),e3,e4∈(1,+∞).
椭圆中,
越大,椭圆越扁,
越小,椭圆越圆,所以
;
双曲线中,
越大,双曲线的开口越阔,所以
.∴e1<e2<e4<e3.
答案:C
例2、求适合下列条件的双曲线的标准方程:
(1)过点
,离心率
的双曲线的标准方程.
解:
①当双曲线焦点在x轴上时,设双曲线方程为
,
,∴标准方程为x2-4y2=1.
②当双曲线的焦点在y轴上时,设双曲线方程为
,
,无解.
∴所求双曲线的标准方程为x2-4y2=1.
(2)中心在原点,焦点在x轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为
.
解:
由题意,设双曲线方程为
,
则c=
a,渐近线y=x.
由点F
到y=x的距离为
,得
,解得
.
∴双曲线方程为
.
例3、求与双曲线
共渐近线,且经过点
的双曲线的标准方程及离心率.
解:
双曲线
的渐近线方程为
.
①当焦点在x轴上时,双曲线可设为
,
代入
得:
,解得
,无解;
②当焦点在y轴上时,双曲线可设为
,
代入
得:
,解得
.
∴双曲线的标准方程为
,离心率
.
例4、如图,设
与定点
的距离和它到直线
:
的距离
的比是常数
(
),求点M的轨迹方程.
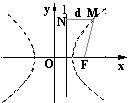
解:
点
的集合为
,
代入坐标有:
.
化简得
.
说明:
可以看出这是双曲线的方程,即点
与定点
的距离和它到定直线
:
的距离比是常数
,则点
的轨迹方程是双曲线.其中定点
是焦点,定直线
:
是相应于F的准线,常数
是离心率;由双曲线的对称性,另一焦点
,相应于
的准线
:
.我们称这个轨迹的定义为双曲线的第二定义.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -