| 电源和电流 |
主编:黄冈中学物理集体备课组
一、电源
维持导体两端有一定电压的装置是电源.电路中的电源能把其它形式的能转化为电能,从而保持电源正负极之间有持续的电压.
二、恒定电场
1、形成:由电源、导线等电路元件所积累的电荷共同形成的.
2、基本性质:与静电场相同.
三、恒定电流
1、概念:大小、方向都不随时间变化的电流.
2、电流:表示电流强弱的物理量.(物理意义)
3、定义:单位时间内通过导体横截面的电荷量.
4、单位:安培(A)
1A=103mA=106μA
5、方向:规定正电荷定向移动的方向为电电流方向.
讲解:①金属导体中:自由电子定向移动与I的方向.
②电解液中:正负离子.
③电流是标量.
6、电流的微观表达式
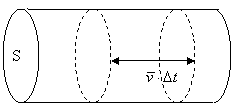
设导体中单位体积内的自由电荷数为n,一个自由电荷的电荷量为q,电荷定向移动的平均速率为
,则
△t时间内能到达S的自由电荷数为
N=n
△t·S
Q= n
△tS·q
的数量级10-5m/s.
例1、关于电流,下列说法中正确的是( )
A.通过导体横截面的电荷量越多,电流越大
B.电子运动速率越大,电流越大
C.单位时间内通过导线横截面的电荷量越多.导体中的电流就越大
D.因为电流有方向,所以电流是矢量
解析:
由
知q大,I不一定大,还要看t的大小,故A错,由I=nqSv知,电子运动的速率v大,电流不一定大,电流还与n、S有关,故B错,单位时间内通过导线横截面的电量越多,电流越大,C对.电流虽有方向但不是矢量,合成遵循代数法则,故D错.
答案:C
点评:
电流由电荷的定向移动形成,从微观表达式来看,I=nqsv,电流与导体中的单位体积的电荷数、电荷的电量、导线的横截面积、定向移动的速度这四个因素有关.电流有大小也有方向但不是矢量,因此它不遵循平行四边形法则.
例2、已知电子的电荷量为e,质量为m,氢原子的电子在核的静电力吸引下做半径为r的匀速圆周运动,则电子运动形成的等效电流大小为多少?
解析:
截取电子运动轨道的任一截面,在电子运动一周的时间T内,通过这个截面的电荷量q=e.则有:
①
再由库仑力提供向心力有:
②
解得
答案:
点评:
解决这个题的关键是选取合适的过程,考虑到电子运动的周期性,选取一个周期是最简洁的.
高一全科点睛班课程 高一全科强化班课程 高二全科全年强化班 高三全科强化班课程 初一全科强化班课程 初一全科点睛班课程 初二全科强化班视频 初二全科点睛班课程 初三全科强化班 全科巨无霸同步提高课程 小学全年全科强化班
- 返回 -