1、如图所示电路中,已知电源的内阻r>R2,电阻R1的阻值小于滑动变阻器R0的最大阻值.闭合电键S,当滑动变阻器的滑臂P由变阻器的右端向左滑动的过程中,下列说法中正确的有( )
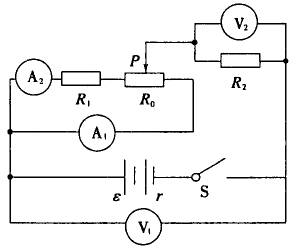
A.V1的示数先变小后变大,V2的示数先变大后变小
B.R2上消耗的功率先变小后变大
C.电源的输出功率先变小后变大
D.A1的示数不断减小,A2的示数不断变大
2、竖直放置的一对平行金属板的左极板上用绝缘线悬挂了一个带正电的小球,将平行金属板按图所示的电路图连接,绝缘线与左极板的夹角为θ,当滑动变阻器R的滑片在a位置时,电流表的读数为I1,夹角为θ1;当滑片在b位置时,电流表的读数为I2,夹角为θ2,则( )
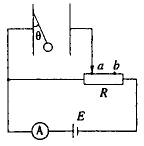
A.θ1<θ2,I1<I2 B.θ1>θ2,I1>I2
C.θ1=θ2,I1=I2 D.θ1<θ2,I1=I2
3、如图电源的内阻不可忽略,已知定值电阻R1=10Ω、R2=8Ω,当电键S连接位置1时,电流表示数为0.20A,那么当S接位置2时,电流表的示数可能是( )
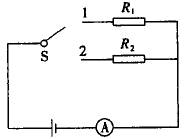
A.0.28A B.0.25A
C.0.22A D.0.19A
显示提示
|
3、电键S接2后,电路的总电阻减小,总电流一定增大,所以电流不可能是0.19A,电源的路端电压一定减小;原来路端电压为2V,所以电键S接2后路端电压低于2V,因此电流一定小于0.25A,故只能选C. |
4、在如下图所示电路中,把R由2Ω变为6Ω时,电流大小减为原来的一半,则电源的内阻为__________Ω.
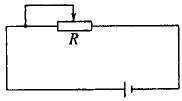
显示答案
5、某同学设计了如图所示电路研究电源输出功率的变化情况.电源E、内电阻恒定,R1为滑动变阻器,R2、R3为定值电阻,  、 、 为理想电表. 为理想电表.
(1)若滑动片P由a滑至b时A示数一直变小,则R1和R2必须满足的关系是__________.
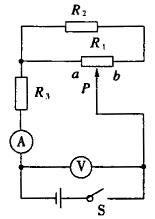
(2)若R1=6Ω,R2=12Ω,电源内电阻r=6Ω,当滑动片P由a滑至b时,电源E的输出功率P随外电路总电阻R的变化关系如图所示,则R3的阻值应选择( )
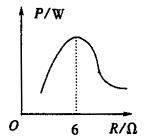
A.2Ω B.4Ω C.6Ω D.8Ω
显示答案
|
5、(1)R1 R2 (2)B R2 (2)B
解析:(1)滑动片P由a滑至b时,A示数一直变小,说明电路中总电阻一直增大,即RPb与R2串联后,又与RaP的并联电阻一直变大,则应满足R1≤R2.
(2)从P-R图像可看出,当R外=6Ω时,电源的输出功率最大,即滑动片从a滑至b的过程中,输出功率先增大后减小,所以R3的阻值不可能大于或者等于6Ω;如果R3=6Ω,则滑动片在a端时输出功率最大,这与图像矛盾.当滑动片在b端时,并联电阻最大,且R并=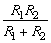 =4Ω,所以R3不可能等于2Ω,若R3=2Ω,则滑动片在b端时输出功率最大,这也与P-R图像矛盾,故R3=4Ω. =4Ω,所以R3不可能等于2Ω,若R3=2Ω,则滑动片在b端时输出功率最大,这也与P-R图像矛盾,故R3=4Ω. |
6、如图所示电路中,已知电阻R1=2Ω,R2=5Ω,灯泡L标有“3V,1.5W”字样,电源内阻r=1Ω,滑动变阻器的最大阻值为Rx.当滑片P滑至a端时,电流表的示数为1A,此时灯泡L恰好正常发光.求:
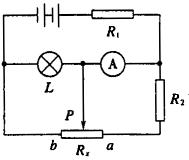
(1)当滑片P滑至b端时,电流表的示数;
(2)当滑动变阻器Pb段的电阻为0.5Rx时,变阻器上消耗的功率.
某同学的部分解答如下:
灯L的电阻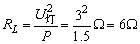 , ,
滑片P滑至b端时,灯L和(Rx+R2)并联,并联电阻为: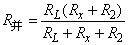
由RL·IA=(Rx+R2)·I2(IA、I2分别为通过电流表和R2的电流)得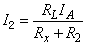
流过电源的电流为I=IA+I2
上述解法是否正确?若正确,请求出最后结果;若不正确,请指出错在何处,纠正后求出最后结果.
显示答案
|
6、解析:灯L的电阻RL=6Ω正确,错在没有看出RPA和R2串联部分已被短路,
E=I(R1+r)+U0=1×(1+2)+3=6(V),
I0=P/U0=0.5A,Ix=I-I0=0.5A,Rx=U0/Ix=6Ω.
(1)当P在B端时,电流表示数为I′=E/(R1+r)=2A,
(2)当RPB=3Ω时,R并=2Ω,
电流表示数为I″=E/(R1+R并+r)=1.2A,
U并=E-I″(R1+r)=2.4V,PR=U2并/RPB=1.92W. |
7、在日常生活中,经常见到这样的现象.手电筒里的电池用旧了舍不得扔掉,买一节新电池与这节旧电池串联使用.测量发现新旧电池的电动势相差不多,而新旧电池的内阻却相差较大.数据如下:
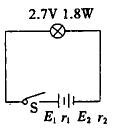
新电池:E1=1.5V,r1=0.3Ω;
旧电池:E2=1.2V,r2=7.8Ω.
已知小灯泡上标有“2.7V 1.8W”,连接如图所示,试探究这样的节约措施可行吗?
显示答案
|
7、解析:新旧电池串联后供电电流:
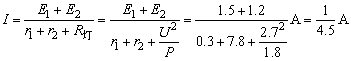 , ,
旧电池提供的总功率P2=1.2×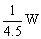 ≈0.27W. ≈0.27W.
旧电池内部消耗功率P2内=I2r2=(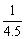 )2×7.8W≈0.39W>0.27W. )2×7.8W≈0.39W>0.27W.
旧电池不能输出电能反而消耗电能,所以新旧电池搭配使用不能达到节约的目的,因此措施不可行. |
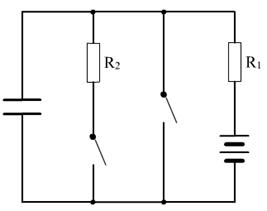
8、已知电源内阻r=2Ω,R1=8Ω,R2=10Ω,S1闭合,S2断开时,相距d=70cm水平放置的固定金属板A、B间,有一质量m=0.1g,q=7×10-5C的微粒恰好静止在两板正中央的位置上.求:
①电源的电动势;
②将S1断开0.1s后又将S2闭合,试求S1断开后,该微粒经多长时间与极板相碰.
显示答案
8、解:①S1闭合,S2断开时,
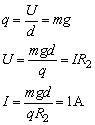
E=I(R1+R2+r)=20V
②开关S1断开的0.1s内
a1=(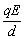 -mg)/m=10m/s2 -mg)/m=10m/s2
h1=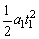 =0.05m<0.35m =0.05m<0.35m
S2闭合后
a2=g
速度减为零的时间
t2=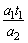 =0.1s =0.1s
h2=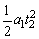 =0.05m =0.05m
h1+h2+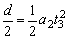
∴t3=0.3s
t总=t1+t2+t3=0.5s时与B极板相碰.
|
|