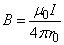1、在计算任意带电体在空间某点的电场强度时,可把带电体分成无限多个电荷元,先求出每个电荷元在该点产生的电场强度,再按场强叠加原理就可以计算出带电体再该点产生的电场强度(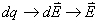 ).对于稳恒电流产生磁场的计算问题,可把稳恒电流分成无限多个电流元,先求出每个电流元在该点产生的磁感应强度,再按场强叠加原理就可以计算出带电体再该点产生的磁感应强度(
).对于稳恒电流产生磁场的计算问题,可把稳恒电流分成无限多个电流元,先求出每个电流元在该点产生的磁感应强度,再按场强叠加原理就可以计算出带电体再该点产生的磁感应强度(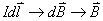 )
)
问题: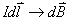 ?
?
2、Biot―Savart―Laplace定律
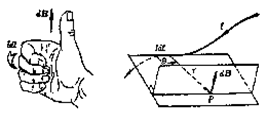
1820年10月30日(在距Oersted报道电流磁效应不到三个月),法国的Biot和Savart在法国科学院发表文章,从实验中分析了电流和磁效应之间的关系.如图所示,小磁针转动强弱反应该点磁感应强度的大小.

实验发现:
1、a大,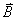 小,
小, .
.
2、I大, 大,
大,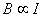 .
.
结论: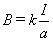
不久,Laplace假定,电流由电流元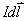 组成:
组成:
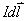 产生的磁感应强度
产生的磁感应强度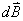 与I成正比;
与I成正比;
磁感应强度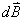 的大小与电流元
的大小与电流元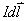 的表观长度
的表观长度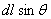 成正比;
成正比;
磁感应强度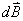 的大小与r的平方成反比.
的大小与r的平方成反比.
在实验上基础上经科学抽象得到:在载流导线上取电流元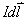 ,空间任一点P,该点的磁感应强度为
,空间任一点P,该点的磁感应强度为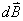 ,
, 与矢径
与矢径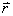 的夹角为θ,实验表明,真空中
的夹角为θ,实验表明,真空中 .
.
在SI制中,k=μ0/4π,其中μ0=4π×10-7N·A-2为真空磁导率.
故 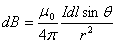 .
.
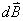 的方向:即
的方向:即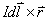 的方向(右手螺旋法则确定)
的方向(右手螺旋法则确定)
写成矢量形式为
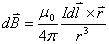
或 
其中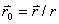 为矢径
为矢径 方向上的单位矢量.
方向上的单位矢量.
这就是Biot―Savart―Laplace定律,也称为Biot―Savart―Laplace定律.
3、任意载流导线在P点的磁感应强度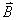 为
为
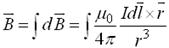
4、说明:
该定律是在实验的基础上抽象出来的,不能由实验直接加以证明,但是由该定律出发得出的一些结果,却能很好地与实验符合.
电流元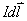 的方向即为电流的方向;
的方向即为电流的方向;
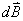 的方向由
的方向由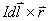 确定,即用右手螺旋法则确定;
确定,即用右手螺旋法则确定;
Biot―Savart―Laplace定律是求解电流磁场的基本公式,利用该定律,原则上可以求解任何稳恒载流导线的磁感应强度.
解题步骤:
根据已知电流的分布与待求场点的位置,选取合适的电流元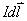 ;
;
选取合适的坐标系.要根据电流的分布与磁场分布的的特点来选取坐标系,其目的是要使数学运算简单;
根据所选择的坐标系,按照Biot―Savart―Laplace定律写出电流元产生的磁感应强度;
由叠加原理求出磁感应强度的分布;
一般说来,需要将磁感应强度的矢量积分变为标量积分,并选取合适的积分变量,来统一积分变量.
典型例题:
两种基本电流周围的磁感应强度的分布:载流直导线;圆电流.
例1、(课本P131)载流长直导线的磁场
(1)一段载流直导线的磁场
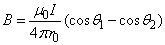
解:建立如图坐标系,在载流直导线上,任取一电流元Idz,由毕—萨定律得元电流在P点产生的磁感应强度大小为:
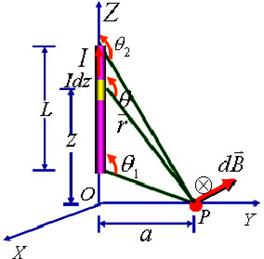
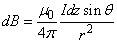
方向为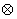 .所有电流元在P点产生的磁场方向相同,所以求总磁感强度的积分为标量积分,即:
.所有电流元在P点产生的磁场方向相同,所以求总磁感强度的积分为标量积分,即:
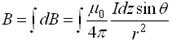 (1)
(1)
由图得:
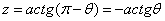 ,
,
因此:dz=acsc2θdθ
此外,
代入(1)可得:
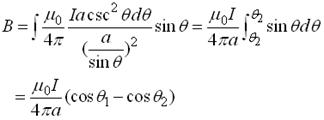
讨论:
(1)无限长直通电导线的磁场: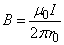
(2)半无限长直通电导线的磁场: