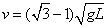例1、某静电场的电场线分布如图所示,图中P、Q两点的电场强度的大小分别为EP和EQ,电势分别为UP和UQ,则( )
A.EP>EQ,UP>UQ
B.EP>EQ,UP<UQ
C.EP<EQ,UP>UQ
D.EP<EQ,UP<UQ
解析:
从图可以看出P点的电场线的密集程度大于Q点的密集程度,故P点的场强大于Q点的场强,因电场线的方向由P指向Q,而沿电场线的方向电势逐渐降低,P点的电势高于Q点的电势,故A项正确.
答案:A
例2、一带负电荷的质点,在电场力作用下沿曲线abc从a运动到c,已知质点的速率是递减的.关于b点电场强度E的方向,下列图示中可能正确的是(虚线是曲线在b点的切线)( )
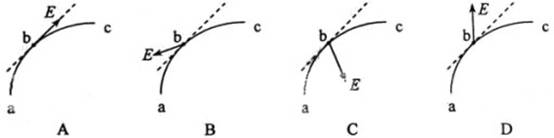
解析:
带点质点在电场力作用下做曲线运动,电场力方向沿电场强度的反方向,又要指向指向曲线的凹测(相当于圆的圆心),又由于速率递减,合力方向与速度方向(轨道切线)的夹角要大于90°.只有D选项所示符合条件.选项D对.本题选D.
答案:D
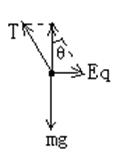
例3、绝缘细绳的一端固定在天花板上,另一端连接着一个带负电的电量为q、质量为m的小球,当空间建立水平方向的匀强电场后,绳稳定处于与竖直方向成θ=60°角的位置,如图所示.

(1)求匀强电场的场强E;
(2)若细绳长为L,让小球从θ=30°的A点释放,王明同学求解小球运动至某点的速度的过程如下:据动能定理―mgL(1-cos30°)+qELsin30°=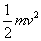 ,得:
,得: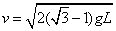 .
.
你认为王明同学求的是最低点O还是θ=60°的平衡位置处的速度,正确吗?请详细说明理由或求解过程.
解析:
(1)小球在θ=60°角处处于平衡,则Eq=mgtanθ
得 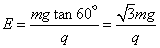 .
.
方向水平向左.
(2)王明同学的求解不正确
因为小球在θ=60°处处于平衡,因此小球从θ=30°的A点释放,它不会往A点的左边运动,而是以θ=60°处为中心、以A点为端点来回摆动,即小球不会运动至最低点O.
王明同学的求解实际上也不是小球运动到θ=60°的平衡位置处的速度.
平衡位置处的速度的正确求解应该是:据动能定理有
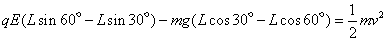
联解得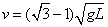
答案:
(1)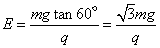 (2)
(2)