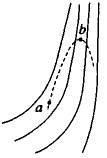
1、如图所示,实线是一个电场中的电场线,虚线是一个负试探电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )
A.电荷从a到b加速度减小
B.b处电势能大
C.b处电势高
D.电荷在b处速度小
显示提示
1、由题图可知b处的电场线比a处的电场线密,说明b处的场强大于a处的场强.根据牛顿第二定律,试探电荷在b处的加速度大于在a处的加速度,A选项错.由题图可知,电荷做曲线运动,必受到不等于零的合外力,即F≠0,且F的方向应指向运动轨迹的凹向.因为试探电荷带负电,所以电场线指向是从疏到密.再利用“电场线方向为电势降低最快的方向”判断a、b处电势高低关系是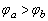 ,C选项不正确.根据试探电荷的位移与所受电场力的夹角大于90°,可知电场力对试探电荷做负功.功是能量变化的量度,可判断由a→b电势能增加,B选项正确.又因电场力做功与路径无关,系统的能量守恒,电势能增加则动能减小,即速度减小,D选项正确. ,C选项不正确.根据试探电荷的位移与所受电场力的夹角大于90°,可知电场力对试探电荷做负功.功是能量变化的量度,可判断由a→b电势能增加,B选项正确.又因电场力做功与路径无关,系统的能量守恒,电势能增加则动能减小,即速度减小,D选项正确. |
2、如图所示,虚线表示电场的一族等势面且相邻等势面电势差相等,一个带正电的粒子以一定的初速度进入电场后,只在电场力作用下沿实线轨迹运动,粒子先后通过M点和N点.在这一过程中,电场力做负功,由此可判断出( )
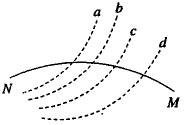
A.N点的电势高于M点的电势
B.粒子在N点的电势能比在M点的电势能大
C.粒子在M点的速率小于在N点的速率
D.粒子在M点受到的电场力比在N点受到的电场力大
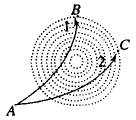
3、如图所示,虚线为某电场的等势面,今有两个带电粒子(重力不计),以不同的速率,沿不同的方向,从A点飞入电场后,沿不同的轨迹1和2运动,由轨迹可以断定( )
A.两个粒子带电量一定不同
B.两个粒子的电性一定不同
C.粒子1的动能和粒子2的电势能都是先减少后增大
D.经过B、C两点,两粒子的速度可能不等
显示提示
|
3、由等势线的形状知,这是一个位于圆心的点电荷产生的电场,两个粒子与点电荷的作用情况是相反的,所以两个粒子电性一定不同.粒子1的动能先减小后增大,粒子2的电势能先减小后增大.到B、C两点时两个粒子的速度可能相同也可能不同,无法确定. |
4、如图所示,一带正电的粒子进入一点电荷+Q的电场中,初速度为v0,轨迹如图所示,则( )
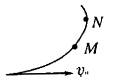
A.N点电势高于M点电势
B.N点电势低于M点电势
C.该粒子在M点动能比在N点动能大
D.该粒子在M点电势能比在N点电势能大
显示提示
|
4、由于带正电的粒子,进入+Q的点电荷所形成的电场中,粒子受到的排斥力一定指向轨迹的凹侧.从曲线的弯曲情况看,M点曲率半径大,N点曲率半径小,说明N点更接近形成电场的点电荷+Q,因此,N点电势高,粒子由M到N电场力做负功,电势能增大,动能减小. |
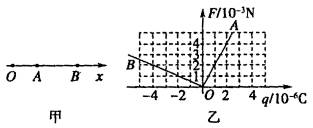
5、某实验小组在研究检验电荷所受电场力跟所带电荷量的关系时,利用测得的数据画出A、B两点的F-q图象如图乙所示,O、A、B为x轴上的三点,位置关系如图甲所示,电场力的正方向与x轴正方向一致,但实验时忘记了验证场源电荷的电性,也忘记了记下场源电荷在x轴上的具体位置.请分析能否判断场源电荷的电性、大致位置及A、B两点电势高低.
显示答案
|
5、由图乙可知,正的检验电荷放在A点负的检验电荷放在B点所受电场力方向均沿x轴正方向,说明场源电荷为负电荷,且放在AB之间,由F-q图线的斜率可知A点场强EA=2×103N/C,B点场强EB=5×102N/C,说明场源电荷离A点较近,所以A点的电势低于B点的电势. |
6、如图所示,一质量为m的塑料球形容器敢在桌面上,它的内部有一劲度系数为k的轻弹簧,弹簧直立地固定于容器内壁的底部,弹簧上端经绝缘体系住一只带正电q、质量也为m的小球.从加一个竖直向上的场强为E的匀强电场起,到容器对桌面压力减为零时为止,求:
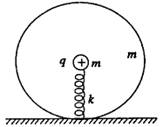
(1)小球的电势能改变量;
(2)容器对桌面压力减为零时小球的速度大小.
显示答案
7、如图所示,直角三角形ABC的斜边倾角为30°,底边BC长2L,处在水平位置,斜边AC是光滑绝缘的,在底边中点O处放置一正电荷Q,一个质量为m、电荷量为q的带负电的质点从斜面顶端A沿斜边滑下,滑到斜边的垂足D时速度为v[将(1)、(2)题正确选项前的标号填在括号内]

(1)在质点的运动中不发生变化的是( )
①动能
②电势能与重力势能之和
③动能与重力势能之和
④动能、电势能、重力势能之和
A.①② B.②③ C.④ D.②
(2)质点的运动是( )
A.匀加速运动
B.匀减速运动
C.先匀加速后匀减速的运动
D.加速度随时间变化的运动
(3)该质点滑到非常接近斜边底端C点时速率vC为多少?此时沿斜面向下的加速度aC为多少?
显示答案
|
7、(1)C
(2)D
(3)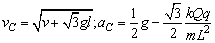
解析:(3)因BD=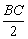 =OC=OD,则B、C、D三点在以O为圆心的同一圆周上,是O点处点电荷Q产生构电场中的等势点,所以,q由D到C的过程中电场力做功为零,由机械能守恒定律: =OC=OD,则B、C、D三点在以O为圆心的同一圆周上,是O点处点电荷Q产生构电场中的等势点,所以,q由D到C的过程中电场力做功为零,由机械能守恒定律:
 ① ①
其中,
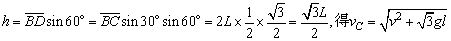 ② ②
质点在C点受三个力的作用:电场力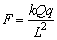 ,方向由C指向O点;重力mg,方向竖直向下;支持力FN,方向垂直于斜向向上,根据牛顿第二定律:mgsinθ-Fcosθ=maC ③ ,方向由C指向O点;重力mg,方向竖直向下;支持力FN,方向垂直于斜向向上,根据牛顿第二定律:mgsinθ-Fcosθ=maC ③
解得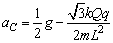 ④ ④ |
|