22、(本题满分12分)函数，g(x)＝1＋loga(x－1)(a>0，且a≠1)，设f(x)和g(x)定义域的公共部分为D．
（1）求集合D；
（2）当a>1时，若不等式在D内恒成立，求a的取值范围；
（3）是否存在实数a，使得时，f(x)在[m，n]上的值域是[g(n)，g(m)]．若存在求a的取值范围；若不存在说明理由．
解：（1）由有：D＝(3，＋∞)．……………… 3分
（2）当a>1时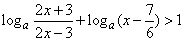，，即在x>3时恒成立，令2x－3＝t(t>3)
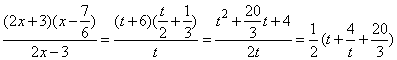……… 5分
当t∈(3，＋∞)时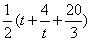，单调递增，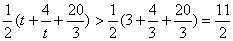
故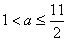……………… 7分
（3）∵m<n时，g(n)<g(m)，∴0<a<1，而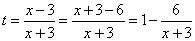在(3，＋∞)上递增．
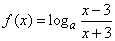∴在[m，n]上递减．
又f(x)在[m，n]上的值域为[g(n)，g(m)]．．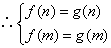
即m，n是方程f(x)＝g(x)的两个根．
∴方程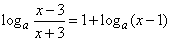在(3，＋∞)上有两个不同实数根．… 9分
方程等价于．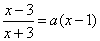
∴ax2＋(2a－1)x＋3－3a＝0在(3，＋∞)上有两个不同实数根．
设F(x)＝ax2＋(2a－1)x＋3－3a．
则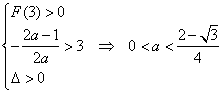．……… 12分
，g(x)＝1＋log
在D内恒成立，求a的取值范围；
时，f(x)在[m，n]上的值域是[g(n)，g(m)]．若存在求a的取值范围；若不存在说明理由．
有：D＝(3，＋∞)．……………… 3分
，即
在x>3时恒成立，令2x－3＝t(t>3)
……… 5分
单调递增，
……………… 7分
在(3，＋∞)上递增．
在[m，n]上递减．
．
在(3，＋∞)上有两个不同实数根．… 9分
．
．……… 12分