解：（1）由已知可得l2的斜率存在，且k2＝1－a．

若k2＝0，则1－a＝0，a＝1．

∵l1⊥l2，直线l1的斜率k1必不存在，即b＝0．

又∵l1过点（－3，－1），∴－3a＋4＝0，即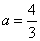（矛盾）．

∴此种情况不存在，∴k2≠0．

即k1，k2都存在，∵k2＝1－a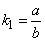，，l1⊥l2，

∴k1k2＝－1，即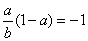．①

又∵l1过点（－3，－1），∴－3a＋b＋4＝0．②

由①②联立，解得a＝2，b＝2．（5分）

（2）∵l2的斜率存在，l1∥l2，∴直线l1的斜率存在，

k1＝k2，即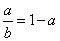．③

又∵坐标原点到这两条直线的距离相等，且l1∥l2，

∴l1，l2在y轴上的截距互为相反数，即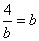，④

联立③④，解得或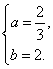

∴a＝2，b＝－2或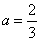，b＝2．（10分）