解：（Ⅰ）f（x）的定义域为（0，＋∞）．

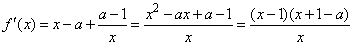（2分）

（i）若a－1＝1即a＝2，则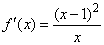，故f（x）在（0，＋∞）单调增加．（3分）

（ii）若a－1＜1，而a＞1，故1＜a＜2，则当x∈（a－1，1）时，f′（x）＜0；

当x∈（0，a－1）及x∈（1，＋∞）时，f′（x）＞0．

故f（x）在（a－1，1）单调减少，在（0，a－1），（1，＋∞）单调增加．（4分）

（iii）若a－1＞1，即a＞2，同理可得f（x）在（1，a－1）单调减少，在（0，1），（a－1，＋∞）单调增加．（5分）

（Ⅱ）令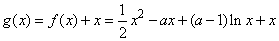

则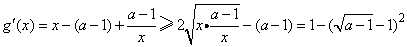

由于1＜a＜5，故g′（x）＞0，即g（x）在（0，＋∞）单调增加，从而当x1＞x2＞0时有g（x1）－g（x2）＞0，即f（x1）－f（x2）＋x1－x2＞0，故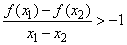，当0＜x1＜x2时，有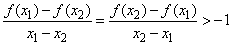．（12分）

考点：用导数研究函数的性质．