解：（1）当a＝－1时，f（x）＝|x－1|＋|x＋1|．由f（x）≥3，得|x－1|＋|x＋1|≥3．

（i）x≤－1时，不等式化为1－x－1－x≥3，即－2x≥3．

不等式组的解集为．

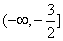（ii）当－1＜x≤1时，不等式化为1－x＋x＋1≥3，不可能成立．

不等式组的解集为．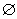

（iii）当x＞1时，不等式化为x－1＋x＋1≥3，即2x≥3．

不等式组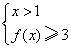的解集为．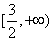

综上得，f（x）≥3的解集为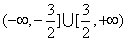．（5分）

（2）若a＝1，f（x）＝2|x－1|，不满足题设条件．

若a＜1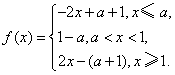，f（x）的最小值为1－a．

若a＞1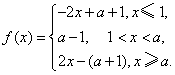，f（x）的最小值为a－1．

所以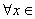R，f（x）≥2的充要条件是|a－1|≥2，从而a的取值范围为（－∞，－1]∪[3，＋∞）．（10分）