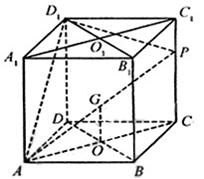
解法一:(1)如图:
 (1分)
(1分)
 故
故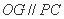 .
.
所以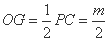 .又
.又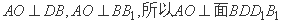 .(3分)
.(3分)
故 .(4分)
.(4分)
在Rt△AOG中,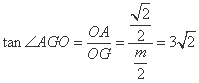 ,即
,即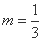 .
.
故当 时,直线
时,直线
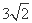 .(6分)
.(6分)
(Ⅱ)依题意,要在A1C1上找一点Q,使得D1Q⊥AP.只需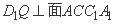 .(7分)
.(7分)
设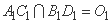 ,可推测A1C1的中点O1即为所求的Q点.(8分)
,可推测A1C1的中点O1即为所求的Q点.(8分)
因为D1O1⊥A1C1,D1O1⊥AA1,所以D1O1⊥面ACC1A1.
即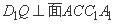 .(10分)
.(10分)
又 ,故D1O1⊥AP.即D1Q⊥AP.(12分)
,故D1O1⊥AP.即D1Q⊥AP.(12分)
解法二:(1)建立如图所示的空间直角坐标系,(1分)
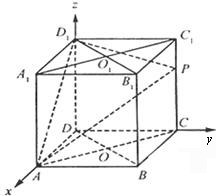
则A(1,0,0), B(1,1,0), P(0,1,m),C(0,1,0), D(0,0,0), B1(1,1,1), D1(0,0,1).
所以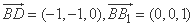 ,
,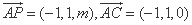 .(2分)
.(2分)
又由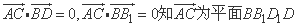 的一个法向量.(3分)
的一个法向量.(3分)
设AP与面BDD1B1所成的角为θ,
则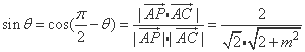 .(4分)
.(4分)
依题意有: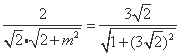 ,解得
,解得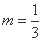 .(5分)
.(5分)
故当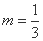 时,直线AP与平面BDD1B1所成的角的正切值为
时,直线AP与平面BDD1B1所成的角的正切值为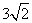 .(6分)
.(6分)
(2)若在A1C1上存在这样的点Q,设此点的横坐标为x,(7分)
则 .(8分)
.(8分)
依题意,对任意的m要使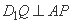 ,只需
,只需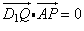 对
对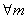 恒成立.(9分)
恒成立.(9分)
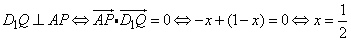 ,(11分)
,(11分)
即Q为A1C1的中点时,满足题设的要求.(12分)