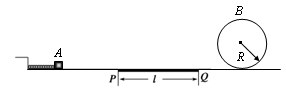
解：（1）设物块冲上圆形轨道最高点B时速度为v，由能量守恒定律得：

Epm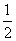＝mv2＋2mgR＋μmgl 　　①（2分）

物块在B点时，重力提供向心力，由牛顿第二定律得：

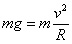　　②（2分）

联立①②式并代入数据解得Epm＝16 J（2分）

• 若要使物块不脱离轨道，分两种情况讨论：

（i）滑块能够通过B点而不脱离轨道，则应满足：l≤1.5m　　③（2分）

（ii）滑块能够到达圆形轨道，则应满足：Epm＞μmgl，解得l＜4m　　④（2分）

滑块到达圆形轨道而又不超过与圆心等高的点C时，如图所示，临界条件取到达C点时速度恰好为零，则有Epm≤mgR＋μmgl，解得l≥3m　　⑤（2分）

综合③④⑤式可得PQ段长度l应满足的条件是：

l≤1.5m或3m≤l＜4m（1分）