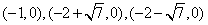解：（1）∵抛物线y＝ax2＋bx＋c（a≠0）与x轴交于点A（1，0）和点B（－3，0），

∴OB＝3，

∵OC＝OB，

∴OC＝3，

∴c＝3，

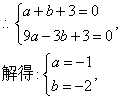
∴所求抛物线解析式为：y＝－x2－2x＋3；

（2）如图2，过点E作EF⊥x轴于点F，设E（a，－a2－2a＋3）（－3＜a＜0），

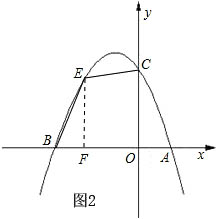
∴BF＝－a2－2a＋3，BF＝a＋3，OF＝－a，

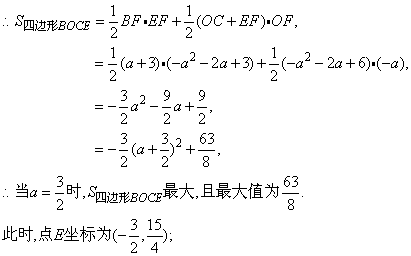
如图3，过A1作A1N⊥对称轴于N，设对称轴与x轴交于点M，

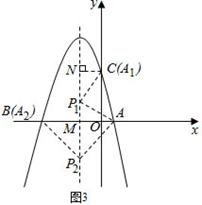
∴∠NPA1＋∠MPA＝∠NA1P＋∠NPA1＝90°，

∴∠NA1P＝∠MPA，

在△A1NP与△PMA中，

，

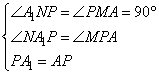∴△A1NP≌△PMA，

∴A1N＝PM＝m，PN＝AM＝2，

∴A1（m－1，m＋2），

代入y＝－x2－2x＋3得：m＋2＝－（x－1）2－2（m－1）＋3，

解得：m＝1，m＝－2（舍去）；

②当m＜0时，要使P2A＝P2A2，由图可知A2点与B点重合，

∵∠AP2A2＝90°，∴MP2＝MA＝2，

∴P2（－1，－2），

∴满足条件的点P的坐标为P（－1，1）或（－1，－2）．

（4）