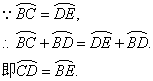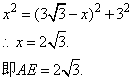字号： 默认 大 中 小
一、选择题（每小题3分，共30分）
1、⊙O的直径AB=4，点C在⊙O上，∠ABC=30°，则AC的长是（ ）
A．1 B．
C．
D．2
2、如图，在5×5正方形网格中，一条弧经过A，B，C三点，则这条弧所在圆的圆心是（ ）
A．点P B．点Q
C．点R D．点M
3、如图，以平行四边形 ABCD的一边AB为直径作⊙O，若⊙O过点C，且∠AOC=70°，则∠A等于（ ）
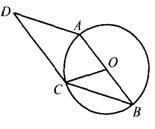
A．145° B．140°
C．135° D．120°
4、如图，A、B、C是⊙O上的三点，∠α=140°，那么∠A等于（ ）
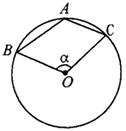
A．70° B．110°
C．140° D．220°
5、点P为⊙O内一点，且OP=4，若⊙O的半径为6，则过点P的弦长不可能为（ ）
A．
B．12
C．8 D．10.5
6、使式子
有意义的x的取值范围是（ ）
A．x≤1 B．x≤1且x≠－2
C．x≠－2 D．x＜1且x≠－2
7、设方程x2＋x－2=0的两个根为α，β，那么（α－2）（β－2）的值等于（ ）
A．－4 B．0
C．4 D．2
8、若关于x的一元二次方程kx2＋2x－1=0有实数根，则k的取值范围是（ ）
A．k＞－1 B．k≥－1
C．k＞－1且k≠0 D．k≥－1且k≠0
9、如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型．若圆的半径为r，扇形的半径为R，扇形的圆心角等于90°，则R与r之间的关系是（ ）
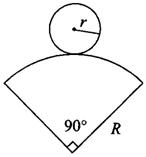
A．R=2r B．
C．R=3r D．R=4r
10、如图所示，已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，经过t秒后，以O、A为顶点作菱形OABC，使B．C点都在第一象限内，且AO=AC，又以
为圆心，PC为半径的圆恰好与OC所在的直线相切，则t=（ ）
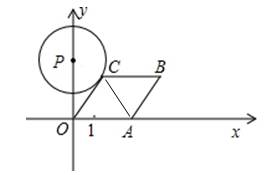
A．
B．
C．5 D．7
二、填空题（每小题3分，共24分）
11、已知⊙O的直径为 6，P为直线l上一点，OP=3，那么直线l与⊙O的位置关系为__________．
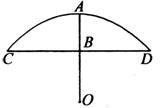
12、如图，有一圆弧形门拱的拱高AB为1m，跨度CD为4m，则这个门拱的半径为__________m．
13、如图，矩形ABCD交⊙O于点A．B．E、F，DE=1cm，EF=3cm，则AB=________cm．
14、在边长为3cm，4cm，5cm的三角形白铁皮上剪下一个最大的圆，此圆的半径为__________cm．
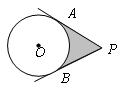
15、如图所示，PA，PB切⊙O于A，B两点，若∠APB=60°，⊙O的半径为3，则阴影部分的面积为__________．
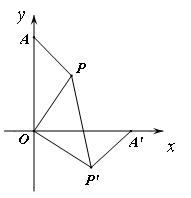
16、如图，在直角坐标系中，点A（0，5），点P（2，3），将△AOP绕点O顺时针方向旋转，使OA边落在x轴上，则点P＇的坐标为__________．
17、已知圆锥的侧面积恰好等于其底面积的2倍，则该圆锥侧面展开图所对应扇形圆心角的度数为__________．
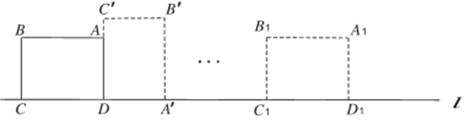
18、如图，矩形ABCD中，AB=8，BC=6，边CD在直线l上，将矩形ABCD沿直线l作无滑动翻滚，当点A第一次翻滚到点A1位置时，则点A经过的路线长为__________．
，∴总路线长为
．三、解答与证明（共66分）
19、解方程（每小题3分，共12分）
（1）（2x－1）2=9 （2）（x＋1）（x＋2）=2x＋4
（3）3x2－4x－1=0 （4）
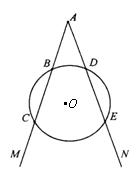
20、（5分）如图，射线AM交一圆于点B、C，射线AN交该圆于点D、E，且
，求证：AB=AD．
21、（5分）某玩具商店根据市场调查，用2 500元购进
一批儿童玩具，上市后很快脱销，接着又用4 500元购进第二批这
种玩具，所购数量是第一批数量的1.5倍，但每套进价多了10元．求第二批玩具每套的进价是多少元？
，
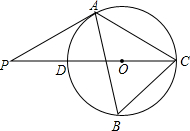
22、（5分）如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．求证：PA是⊙O的切线．
23、（7分）某市自来水公司为鼓励居民节约用水，采取按月用水量分段收费的办法，若某户居民应交水费y（元）与用水量x（吨）的函数关系如图所示．
（1）分别写出当0≤x≤15和x≥15时，y与x的函数关系式；
（2）若某用户该月应交水费42元，则该月用水多少吨？
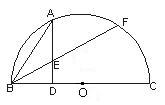
显示答案与解析
；24、（8分）如图，BC是圆O的直径，AD垂直BC于D，
，BF与AD交于E，求证：（1）AE=BE；（2）若A，F把半圆三等分，BC=12，求AE的长．
，
，
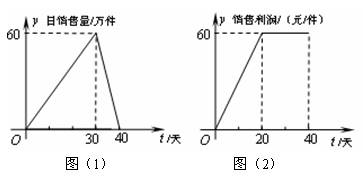
25、（12分）某公司专销产品A，第一批产品A上市40天内全部售完、该公司对第一批产品A上市后的市场销售情况进行了跟踪调查，调查结果如图所示，其中图25（1）中的折线表示的是市场日销售量与上市时间的关系；图25（2）中的折线表示的是每件产品A的销售利润与上市时间的关系．
（1）写出第一批产品A的市场日销售量y与上市时间t的关系式；
（2）写出每件产品A的销售利润y与上市时间t的关系式；
（3）第一批产品A上市后，哪一天这家公司市场日销售利润最大？最大利润是多少万元？
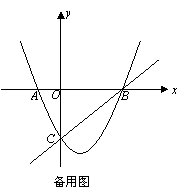
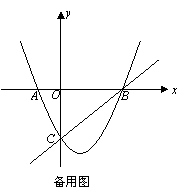
26、（12分）如图，在平面直角坐标系中，二次函数y=x2＋bx＋c的图象与x轴交于A．B两点，A点在原点的左则，B点的坐标为（3，0），与y轴交于C（0，－3）点，点P是直线BC下方的抛物线上一动点．
（1）求这个二次函数的表达式；
（2）求出四边形ABPC的面积最大时的P点坐标和四边形ABPC的最大面积；
（3）连结PO、PC，在同一平面内把△POC沿y轴翻折，得到四边形POP′C，是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由；
（4）在直线BC找一点Q，使得△QOC为等腰三角形，请直接写出Q点坐标．
