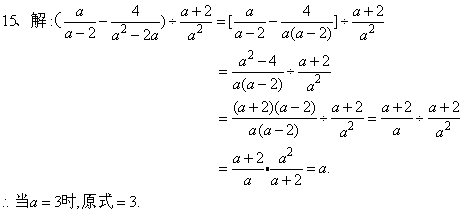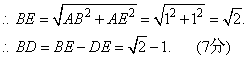字号: 默认 大 中 小
时间:120分钟 满分:120分
一、选择题(共7小题,每小题3分,满分21分)
1、实数-2016的相反数是( )
A.2016 B.-2016
C.±2016 D.
2、下列各数中是有理数的是( )
A.
B.4π
C.sin45° D.
3、下列计算中,不正确的是( )
A.-2x+3x=x B.6xy2÷2xy=3y
C.(-2x2y)3=-6x6y3 D.2xy2·(-x)=-2x2y2
4、一种细胞的直径为0.00000156米,将0.00000156用科学记数法表示应为( )
A.1.56×106 B.1.56×10-6
C.1.56×10-5 D.1.56×10-4
5、已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a>2 B.a<2
C.a>-2且a≠1 D.a<2且a≠1
6、如图,将三角尺的直角顶点放在直线a上,a∥b,∠1=50°,∠2=60°,则∠3的度数为( )
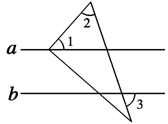
A.50° B.60°
C.70° D.80°
7、二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2-4ac与反比例函数![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )

二、填空题(共7小题,每小题3分,满分21分)
8、计算:![]() __________.
__________.
9、已知a-b=2,ab=1,则a2b-ab2的值为__________.
10、不等式组 的解集是__________.
的解集是__________.
11、若关于x的方程![]() 无解,则m的值为__________.
无解,则m的值为__________.
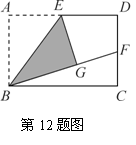
12、如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F.若CF=1,FD=2,则BC的长为__________.
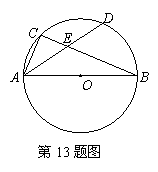
13、如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=10,AD=8,则AE的长为__________.
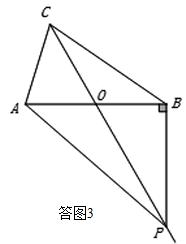
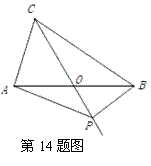
14、如图,在△ABC中,AB=BC=2,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为__________.
三、解答题(共10小题,满分78分)
15、(满分6分)先化简,后求值:![]() ,其中a=3.
,其中a=3.
16、(满分7分)某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长.已知该养殖户第一年的可变成本为3万元,如果该养殖户第三年的养殖成本为7.63万元,求可变成本平均每年增长的百分率.
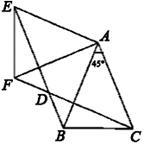
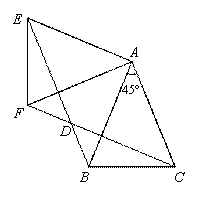
显示答案与解析17、(满分7分)如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
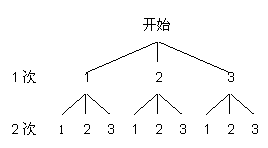
18、(满分6分)现有形状、大小和颜色完全一样的三张卡片,上面分别标有数字“1”、“2”,“3”,第一次从这三张卡片中随机抽取一张,记下数字后放回,第二次再从这三张卡片中随机抽取一张并记下数字,请用列表或画树状图的方法表示出上述试验所有可能的结果,并求第二次抽取的数字大于第一次抽取的数字的概率.
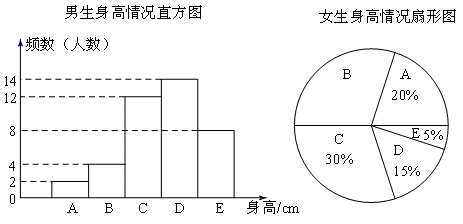
显示答案与解析19、(满分7分)为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制如图所示的统计图表.
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在__________组(填组别序号),女生身高在B组的人数有__________人;
(2)在样本中,身高在150≤x<155之间的人数共有__________人,身高人数最多的在__________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
组别 |
身高(cm) |
A |
x<150 |
B |
150≤x<155 |
C |
155≤x<160 |
D |
160≤x<165 |
E |
x≥165 |
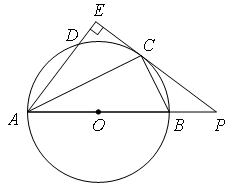
20、(满分7分)如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB∶PC=1∶2.
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由.
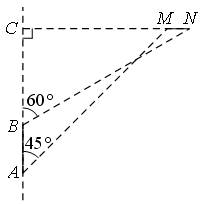
21、(满分6分)钓鱼岛自古就是中国的领土.某日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为16km(即MC=16km).在A点测得岛屿的西端点M在点A的东北方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东60°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果保留根号).
23、(满分10分)甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时).图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图象(线段AB表示甲出发不足2小时因故停车检修).请根据图象所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)求乙车出发多长时间,两车在途中第一次相遇?

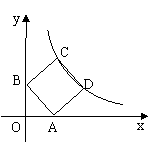
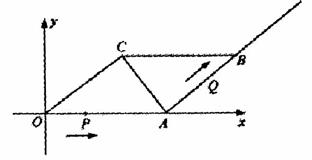
24、(满分15分)已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从O点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动. 设移动的时间为t秒.
(1)求经过O,A,C三点的抛物线的解析式;
(2)在(1)中抛物线的对称轴上找一点M使△MAC的周长最小,求出点M的坐标;
(3)试求出当t为何值时,△OAC与△PAQ相似;
(4)是否存在某一时刻,使△PAQ为等腰三角形?若能,请直接写出t的所有可能的值;若不能,请说明理由.
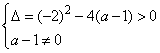 ,解得:a<2且a≠1.
,解得:a<2且a≠1.