字号： 默认 大 中 小
(考试时间120分钟 满分120分)
第Ⅰ卷(选择题 共24分)
一、选择题（下列各题的备选答案中，有且仅有一个答案是正确的，每小题3分，共24分)
1．计算：
＝（ ）
A．9 B．3
C．－3 D．±3
2．设直角三角形的两条直角边分别为a和b，斜边长为c．已知b＝12，c＝13，则a＝（ ）
A．1 B．5
C．10 D．25
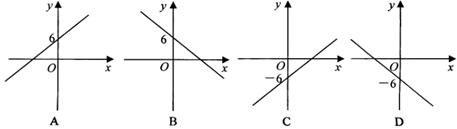
3．一次函数y＝kx－6(k＜0)的图象大致是（ ）
4．下列图形中，不一定是轴对称图形的是（ ）
A．平行四边形 B．矩形
C．菱形 D．正方形
5．下列定理的逆命题为假命题的是（ ）
A．两直线平行，内错角相等
B．直角三角形的两锐角互余
C．角平分线上的点到角两边的距离相等
D．对顶角相等
6．在一次打靶训练中，甲、乙两人在相同的条件下，各射靶10次．已知甲、乙射击的成绩的平均数都是8环，甲的方差是1.2，乙的方差是1.9．下列说法中不一定正确的是（ ）
A．甲、乙射击的总环数相同
B．甲的成绩比乙稳定
C．乙的成绩比甲的波动性大
D．甲、乙射击环数的众数相同
7．已知实数a在数轴上的位置如图所示，则化简|a－1|＋
的结果是（ ）
A．－1 B．1
C．1－2a D．2a－1
8．甲、乙两艘客轮同时离开港口，航行速度都是40米／分钟．甲客轮用30分钟到达A处，乙客轮用40分钟到达B处．若A，B两处的直线距离为2000米，甲客轮沿着北偏东30°的方向航行，则乙客轮的航行方向可能是（ ）
A．北偏西30° B．南偏西30°
C．南偏东60° D．南偏西60°
第Ⅱ卷(非选择题 共96分)
二、填空题(共7小题，每小题3分，共21分)
9．若式子
在实数范围内有意义，则x应满足的条件是_________．
10．数据：3，5，5，4，6，3，5的众数是_________．
11．把
化为最简二次根式，结果是_________．
12．红星中学食堂有存煤100吨，每天用去2吨，x天后还剩下煤y吨，则y(吨)随x(天)变化的函数解析式为_________．
13．已知：四边形ABCD是菱形，两条对角线的长分别为AC＝10，BD＝24，则边长AB的长为_________．
14．在平面直角坐标系中，把直线y＝x向左平移一个单位长度后，得到直线的解析为_________．
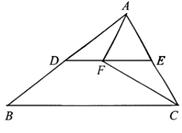
15．如图，在△ABC中，点D，点E分别是AB，AC的中点，点F是DE上一点，∠AFC＝90°．BC＝10cm，AC＝6cm，则DF＝_________cm．
三、解答题(本大题共10分，满分共75分)
；
．
．………4分17．(本题满分7分)先化简，再求值：
，其中
．
时，原式＝
．………6分
19．(本题满分9分)已知一次函数y＝kx＋b的图象经过点A(0，2)和点B(1，3)．
(1)求此一次函数的解析式；
(2)若一次函数y＝kx＋b的图象与x轴相交于点C，求点C的坐标．
(3)求△OAB的面积．
解得
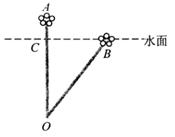
×2×1＝1．………9分20．(本题满分8分)池塘中有一株荷花的茎长为OA，无风时露出水面部分CA＝0.4米．如果把这株荷花向旁边拉至使它的顶端A恰好到达池塘的水面B处，此时荷花顶端离原来位置的距离BC＝1.2米. 求这棵荷花的茎长OA.
．
－4．
BE＝
（4
－4）＝4－2
．……8分22．(本题满分8分)城东中学七年级举行跳绳比赛，要求每班选派5名学生参加．在规定时间每人跳绳不低于150次为优秀，冠、亚军将在甲、乙两班中产生．下表是这两个班的5名学生的比赛数据(单位：次)：
根据以上信息，解答下列问题：
(1)写出表中a的值和甲、乙两班的优秀率；
(2)写出两班比赛数据的中位数；
(3)你认为冠军奖状应发给哪个班?简要说明理由．
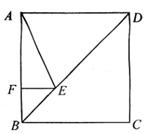
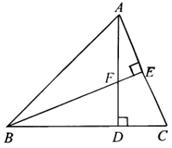
23．(本题满分8分)如图，△ABC中，AB＝BC，∠ABC＝45°，BE⊥AC于点E，AD⊥BC于点D，BE与AD相交于F．
(1)求证：BF＝AC；
(2)若CD＝3，求AF的长．
CD＝
．
．……8分24．(本题满分12分)A城有某种农机30台，B城有该农机50台，现将这些农机全部运往C，D两乡，调运任务承包给某运输公司．已知C乡需要农机36台，D乡需要农机44台．从A城往C，D两乡运送农机的费用分别为220元／台和200元／台，从B城往C，D两乡运送农机的费用分别为180元／台和240元／台．
(1)设A城运往C乡该农机x台，运送全部农机的总费用为W元，求W关于x的函数解析式，并写出自变量x的取值范围；
(2)现该运输公司要求运送全部农机的总费用不低于18160元，则有多少种不同的调运方案?将这些方案设计出来；
(3)现该运输公司决定对A城运往C乡的农机，从运输费中每台减免a元(a≤200)作为优惠，其它费用不变．如何调运，才能使总费用最少?