字号： 默认 大 中 小
本试卷共4页，三大题22小题．全卷满分150分．考试用时120分钟．
一、选择题（本大题共12小题，每小题5分，共60分．在每小题所给的四个选项中，只有一项是符合题目要求的）
1、已知集合M＝{y|y＝cosx，x∈R}，
，则M∩N为（ ）
A．
B．{0，1}
C．{－1，1} D．（－1，1]
2、已知a，b，c∈R，那么下列命题中正确的是（ ）
A．若a＞b，则ac2＞bc2
B．若a3＞b3且ab＜0，则
C．若
，则a＞b
D．若a2＞b2且ab＞0，则
3、已知点（－3，－1）和点（b，－4）均在直线3x－2y－a＝0上，则ab的值为（ ）
A．
B．－35
C．35 D．
4、下列命题错误的是（ ）
A．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β
B．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β
C．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥平面γ
D．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β
5、已知等比数列{an}的公比q≠1，则下面说法中不正确的是（ ）
A．{an＋2＋an}是等比数列
B．对于k∈N*，k＞1，ak－1＋ak＋1≠2ak
C．对于n∈N*，都有anan＋2＞0
D．若a2＞a1，则对于任意n∈N*，都有an＋1＞an
6、下列命题中，正确的命题的是（ ）
A．已知
，则f（x）的最小值是
B．已知数列{an}的通项公式为
，则{an}的最小项为
C．已知实数x，y满足x＋y＝2，则xy的最大值是1
D．已知实数x，y满足xy＝1，则x＋y的最小值是2
7、在数列{an}中，
，anan＋2＝1，则a2016＋a2017＝（ ）
A．5 B．
C．
D．
8、函数y＝asinx－bcosx的一条对称轴为
，则直线l：ax－by＋c＝0的倾斜角为（ ）
A．45° B．60°
C．120° D．135°
9、已知直四棱柱ABCD—A1B1C1D1中，底面ABCD为正方形，AA1＝2AB，E为AA1的中点，则异面直线BE与CD1所成角的余弦值为（ ）
A．
B．
C．
D．
10、设两条直线的方程分别为x＋y＋a＝0，x＋y＋b＝0，已知a、b是关于x的方程x2＋x＋c＝0的两个实数根，且
，则这两条直线之间的距离的最大值和最小值分别为（ ）
A．
B．
C．
D．
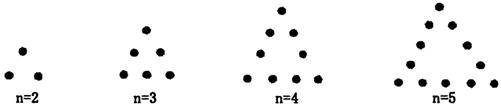
11、如下图所示将若干个点摆成三角形图案，每条边（包括两个端点）有n（n＞1，n∈N*）个点，相应的图案中总的点数记为an，则
（ ）
A．
B．
C．
D．
12、已知曲线
与直线y＝2x＋m有两个交点，则m的取值范围是（ ）
A．（－∞，－4）∪（4，＋∞） B．（－4，4）
C．（－∞，－3）∪（3，＋∞） D．（－3，3）
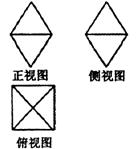
13、一个几何体的三视图如下图所示，若其正视图、侧视图的轮廓都是边长为1的菱形，俯视图是边长为1的正方形，则该几何体的体积为__________．
14、设0＜x＜1，函数
的最小值为__________．
15、已知实数x，y满足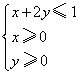
，则
的取值范围是__________．
16、在平面直角坐标系中，设△ABC的顶点分别为A（0，a），B（b，0），C（c，0），点P（0，p）在线段AO上（异于端点），设a、b、c、p均为非零实数，直线BP，CP分别交AC、AB于点E、F，一同学已正确算得OE的方程：
，请你求OF的方程：
．
三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）
17、（本题满分10分）
已知两条直线l1：ax－by＋4＝0和l2：（a－1）x＋y＋b＝0，求满足下列条件的a，b的值：
（1）l1⊥l2，且l1过点（－3，－1）；
（2）l1∥l2，且坐标原点到这两条直线的距离相等．
18、（本题满分12分）
设△ABC的内角A，B，C的对边分别为a，b，c，a＝btanA，且B为钝角．
（1）求B－A的值；
（2）求sinA＋sinC的取值范围．
19、（本题满分12分）
已知：数列{an}满足
，n∈N*．
（1）求数列{an}的通项；
（2）设
，求数列{bn}的前n项和Sn．
20、（本题满分12分）某客运公司用A、B两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次．A、B两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆，公司拟组建一个不超过21辆车的客运车队，并要求B型车不多于A型车7辆．若每天运送人数不少于900，且使公司从甲地去乙地的营运成本最小，那么应配备A型车、B型车各多少辆？
21、（本题满分12分）对于函数f（x），若存在x0∈R，使f（x0）＝x0，则称x0是f（x）的一个不动点，已知函数f（x）＝ax2＋（b＋1）x＋（b－1）（a≠0），
（1）当a＝1，b＝－2时，求函数f（x）的不动点；
（2）对任意实数b，函数f（x）恒有两个相异的不动点，求a的取值范围；
（3）在（2）的条件下，若y＝f（x）的图象上A，B两点的横坐标是f（x）的不动点，且A，B两点关于直线
对称，求b的最小值．
22、（本题满分12分）
如图，在底面是正方形的四棱锥P—ABCD中，PA⊥底面ABCD，BD与AC相交于点E，F为PC中点，G为AC上一点．
（1）求证：BD⊥FG；
（2）确定G在AC上的位置，使得FG∥平面PBD，并说明理由；
（3）当二面角B—PC—D的大小为
时，求PC与底面ABCD所成角的正切值．
