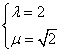字号: 默认 大 中 小
第Ⅰ卷 选择题
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1、复数![]() 在复平面上对应的点位于( )
在复平面上对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2、已知a∈R,则“a>3”是“a2>3a”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
3、设{an}为等差数列,公差d=-2,Sn为其前n项和,若S10=S11,则a1=( )
A.18 B.22
C.20 D.24
4、已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-3,则f(-2)=( )
A.1 B.-1
C.
D.
5、下图给出的是计算![]() 的值的一个程序框图,其中判断框内应填入的条件是( )
的值的一个程序框图,其中判断框内应填入的条件是( )
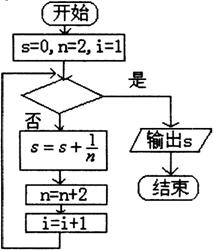
A.i>10? B.i<10?
C.i>20? D.i<20?
6、将函数f(x)=sin(2x+φ)的图象向左平移![]() 个单位,所得到的函数图象关于y轴对称,则φ的一个可能取值为( )
个单位,所得到的函数图象关于y轴对称,则φ的一个可能取值为( )
A.
B.0
C.
D.
7、求曲线y=x2与y=x所围成图形的面积,其中正确的是( )
8、设l,m,n为三条不同的直线,α为一个平面,下列命题中正确的个数是( )
①若l⊥α,则l与α相交
②若m
α,n
α,l⊥m,l⊥n,则l⊥α
③若l∥m,m∥n,l⊥α,则n⊥α
④若l∥m,m⊥α,n⊥α,则l∥n
A.1 B.2
C.3 D.4
9、如图,已知![]() ,点C在线段AB上,且∠AOC=30°,设
,点C在线段AB上,且∠AOC=30°,设![]() ,则
,则![]() 等于( )
等于( )
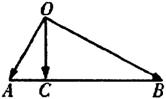
A.
B.3
C.
D.
10、已知曲线C:y=2x2,点A(0,-2)及点B(3,a),从点A观察点B,要使视线不被曲线C挡住,则实数a的取值范围是( )
A.(4,+∞) B.(-∞,4)
C.(10,+∞)D.(-∞,10)
11、某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,左视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )
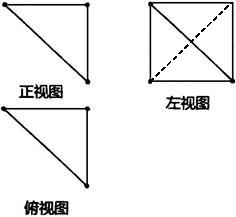
A.
B.4
C.
D.
12、设函数f(x)在R上存在导数f′(x),![]() ,有f(-x)+f(x)=2x2,在(0,+∞)上f′(x)>2x,若f(2-m)+4m-4≥f(m),则实数m的取值范围为( )
,有f(-x)+f(x)=2x2,在(0,+∞)上f′(x)>2x,若f(2-m)+4m-4≥f(m),则实数m的取值范围为( )
A.-1≤m≤1 B.m≤1
C.-2≤m≤2 D.m≥2
第Ⅱ卷 非选择题
二、填空题:本大题共4小题,每小题5分,共20分.
13、已知关于x的二项式![]() 展开式的二项式系数之和为32,常数项为80,则实数a的值为__________.
展开式的二项式系数之和为32,常数项为80,则实数a的值为__________.
14、变量x、y满足条件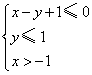 ,则(x-2)2+y2的最小值为__________.
,则(x-2)2+y2的最小值为__________.
15、△ABC的内角A,B,C所对的边分别为a,b,c,且a,b,c成等比数列,若![]() ,
,![]() ,则a+c的值为__________.
,则a+c的值为__________.
16、设a为实常数,y=f(x)是定义在R上的奇函数,且当x<0时,![]() .若f(x)≥a+1对一切x≥0成立,则a的取值范围是__________.
.若f(x)≥a+1对一切x≥0成立,则a的取值范围是__________.
三、解答题(17—21为必做题)
17、(本小题满分12分)已知数列{an}中,a1=3,a2=5且数列{an}的前n项和Sn满足Sn+Sn-2=2Sn-1+2(n≥3);
显示答案与解析(1)求证:{an}为等差数列;
(2)记数列
,求数列{bn}的前n项和Tn.
18、(本小题满分12分)将函数![]() 图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移
图像上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移![]() 个单位长度得到y=sinx的图像.
个单位长度得到y=sinx的图像.
(1)求函数f(x)的解析式;
(2)当x∈[0,3π]时,方程f(x)=m有唯一实数根,求m的取值范围.
显示答案与解析19、(本小题满分12分)已知函数f(x)=x3-3ax2+3a2x-a3(a∈R)的图像关于点(1,0)成中心对称.
(1)确定f(x)的解析式;
(2)求函数g(x)=f(x)-2x2在[-1,1]上的最大值和最小值.
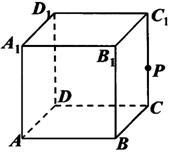
显示答案与解析20、(本小题满分12分)如图,在棱长为1的正方体ABCD—A1B1C1D1中,P是侧棱CC1上的一点,CP=m;
(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为![]() ;
;
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q垂直于AP,并证明你的结论.
21、(本小题满分12分)已知函数f(x)=xln(ax)(a>0)
(1)若![]() 对任意的x>0恒成立,求实数a的取值范围;
对任意的x>0恒成立,求实数a的取值范围;
(2)当a=1时,设函数f(x)的极值点为x0,若实数m,n满足x0<m<1,x0<n<1,且m+n<1.求证: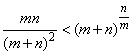 .
.
四、选修题:(请考生在下列22题、23题、24题中任选一题作答,多选以所选第一题的解答给分)
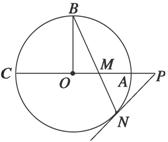
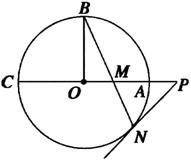
22、(本小题满分10分)如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N点的切线交CA的延长线于点P;
(1)求证:PM2=PA·PC;
(2)若MN=2,![]() ,求劣弧长BN.
,求劣弧长BN.
23、(本小题满分10分)将单位圆经过伸缩变换φ:![]() 得到曲线C:
得到曲线C:![]() ;
;
(1)求实数λ,μ的值;
(2)以原点O为极点,x轴为极轴建立极坐标系,将曲线C上任意一点到极点的距离ρ(ρ≥0)表示为对应极角θ(0≤θ<2π)的函数,并探求θ为何值时,ρ取得最小值?
显示答案与解析24、(本小题满分10分)已知a,b,c∈R+,求证:![]() .
.

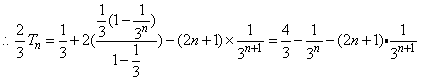 (10分)
(10分)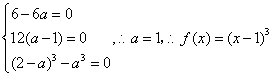 (6分)
(6分)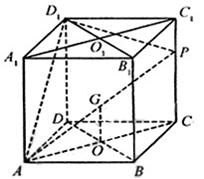
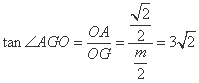 ,即
,即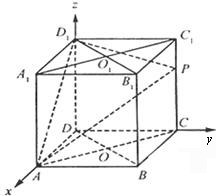
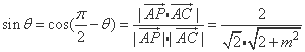 .(4分)
.(4分)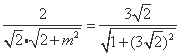 ,解得
,解得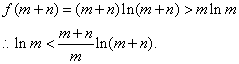
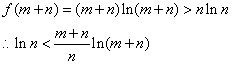
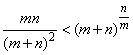 ,即证.
,即证.