字号: 默认 大 中 小
试卷满分150分 考试用时120分钟
第I卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集U=R,集合A={x|y=![]() },B={x|x2-2x<0},则A∪(
},B={x|x2-2x<0},则A∪(![]() )=( )
)=( )
A.[-1, 0] B.[1, 2]
C.[0, 1] D.(-∞,1]∪[2,+∞)
2.已知向量![]() =(2m+1,3,m-1),
=(2m+1,3,m-1),![]() =(2,m,-m),且
=(2,m,-m),且![]() ∥
∥![]() ,则实数m的值等于( )
,则实数m的值等于( )
A.
B.-2
C.0 D.
或-2
3.已知复数z满足(1-2i)z=|1+2i|·(1-i),则复数z的虚部为( )
A.
B.
C.
D.-i
4.将函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,所得图像对应的函数( )
个单位长度,所得图像对应的函数( )
A.在区间
上单调递增
B.在区间
上单调递增
C.在区间
上单调递减
D. 在区间
上单调递减
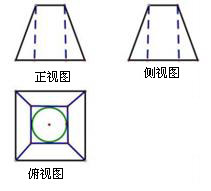
5.已知一个几何体的三视图如图所示,正视图和侧视图是两个的全等的等腰梯形,梯形上底、下底分别为2,4,腰长为![]() ,则该几何体的体积为( )
,则该几何体的体积为( )
A.
B.28-2π
C.28-3π D.
6.已知某产品质量指标服从正态分布 N(200,25),某用户购买了 10000 件这种产品,记 X 表示 10000 件这种产品中质量指标值大于 210 的产品件数,则随机变量 X 的数学期望 EX=( )
附:(随机变量ξ服从正态分布N(μ,δ2),则P(μ-δ<ξ<μ+δ)=68.26%,P(μ-2δ<ξ<μ+2δ)=95.44%)
A.6826 B.3174
C.228 D.456
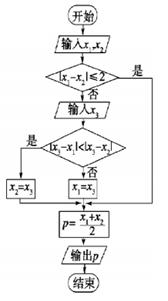
7.图中x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,p为该题的最终得分,当x1=6,x2=9,p=8.5时,x3等于( )
A.11 B.8.5
C.8 D.7
8.设α,β,γ为不同的平面,m,n,l为不同的直线,则m⊥β的一个充分条件为( )
A.α⊥β,α∩β=l,m⊥l
B.α∩γ=m,α⊥γ,β⊥γ
C.α⊥γ,β⊥γ,m⊥α
D.n⊥α,n⊥β,m⊥α
9.数列{an}是等差数列,若 a1+2,a5+5,a9+8 构成公比为 q 的等比数列,则 q=( )
A.-1 B.1
C.±1 D.2
10.某同学准备参加学校组织的“社区卫生服务”、“进福利院演出慰问”、“参观伊利工厂”、“游学遗爱湖公园”、“市中心环保宣传”五个项目的社会实践活动,每天只安排一项活动,并要求在周一至周五内完成.其中“参观伊利工厂”与“市中心环保宣传”两项活动必须安排在相邻两天,“游学遗爱湖公园”活动不能安排在周一.则不同安排方法的种数是( )
A.48 B.24
C.36 D.64
11. 1+7+72+…+72016被6除所得的余数为( )
A.0 B.1
C.2 D.3
12. 已知椭圆E:![]() ,过焦点(0,2)的直线l与椭圆交于M,N两点,点A坐标为(0,
,过焦点(0,2)的直线l与椭圆交于M,N两点,点A坐标为(0,![]() ),
),![]() ,则直线l斜率为( )
,则直线l斜率为( )
A.
B.
C.
D.
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4个小题,每小题5分,共20分.
13.已知实数 x, y 满足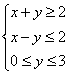 ,则z=2x-y的取值范围是__________.
,则z=2x-y的取值范围是__________.
14.已知函数 f (x)=xa的图象过点 (4,2) ,令![]() ,n∈N*,记数列{an}的前n项和为Sn,则S99=___________.
,n∈N*,记数列{an}的前n项和为Sn,则S99=___________.
15.双曲线![]() 的两条渐近线与圆:(x-3)2+y2=1都相切,则双曲线C的离心率是_____.
的两条渐近线与圆:(x-3)2+y2=1都相切,则双曲线C的离心率是_____.
16.已知函数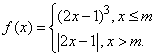 ,若存在实数a,使得函数g(x)=f(x)-a有两个零点,则m的取值范围是___________.
,若存在实数a,使得函数g(x)=f(x)-a有两个零点,则m的取值范围是___________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分 12 分)设ΔABC的三个内角A,B,C所对的边长分别为a,b,c.平面向量![]() =(cos A,cos C),
=(cos A,cos C),![]() = (c,a),
= (c,a),![]() =(2b,0),且
=(2b,0),且![]() ·(
·(![]() -
-![]() )=0.
)=0.
(Ⅰ)求角A的大小;
(Ⅱ)若b=1,a=2,D是边BA上一点且∠B=∠DCA,求CD.
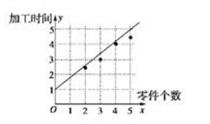
显示答案与解析18.(本小题满分 12 分)某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:

(Ⅰ)在给定的坐标系中画出表中数据的散点图;两个变量y与x的回归模型中,分别选择了2个不同模型,模型①:![]() ,模型②:
,模型②:![]() ,求
,求![]() ,
,![]() ,
,![]() ,
,![]() (精确到0.1);
(精确到0.1);
(Ⅱ)比较两个不同的模型的相关指数R12,R22,指出哪种模型的拟合效果最好,并说明理由.

附:回归方程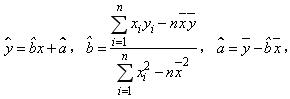 其中
其中![]() ,
,![]() 为样本平均数,令z=
为样本平均数,令z=![]() ,则
,则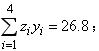
![]() ,
,![]() ,
,![]() ,
,![]() ;
;

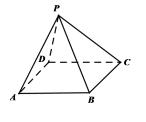
19.(本小题满分 12 分) 如图,四棱锥P-ABCD的底面ABCD是棱长为2的菱形,∠DAB=![]() ,侧面PAD为等边三角形,PB=
,侧面PAD为等边三角形,PB=![]() .
.
(Ⅰ)证明:AD⊥PB;
(Ⅱ)求二面角A-PB-C平面角的余弦值.
20.(本小题满分 12 分)已知抛物线x2=2py (p>0)过点(0,4),作直线l交抛物线于A,B两点,且以AB为直径的圆过原点O.
(Ⅰ)求抛物线方程;
(Ⅱ)若ΔMNP的三个顶点都在抛物线x2=2py上,且以抛物线的焦点为重心,求ΔMNP面积的最大值.
显示答案与解析请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答题时请用2B铅笔在答题卡上把所选题目的题号涂黑.
22.(本小题满分 10 分) 选修 4-1 :几何证明选讲
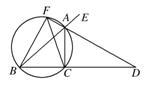
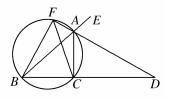
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(Ⅰ)求证:FB2=FA·FD;
(Ⅱ)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6 cm,求AD的长.
23.(本小题满分 10 分) 选修 4-4:坐标系与参数方程
直线l的极坐标方程为![]() ,曲线C参数方程为
,曲线C参数方程为![]() (θ为参数),已知C与l有且只有一个公共点.
(θ为参数),已知C与l有且只有一个公共点.
(Ⅰ)求a的值;
(Ⅱ)过P点作平行于l的直线交C于A,B两点,且|PA|·|PB|=3,求点P轨迹的直角坐标方程.
显示答案与解析24.(本小题满分 10 分)选修 4-5:不等式选讲
对于任意实数a(a≠0)和b,不等式![]() 恒成立,
恒成立,
(Ⅰ)求满足条件的实数x的集合A;
(Ⅱ)是否存在x,y,z∈A,使得x+y+z=1,且![]() 同时成立.
同时成立.
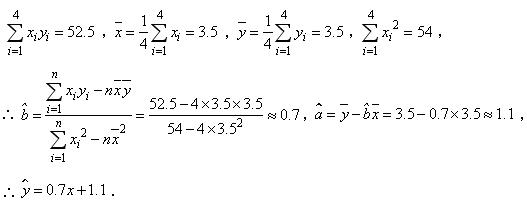
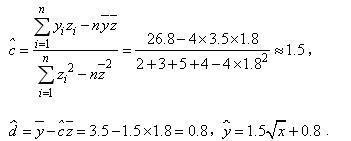
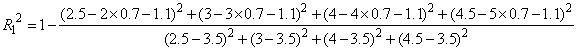
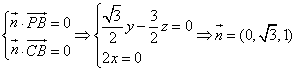
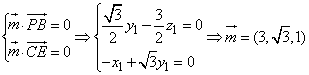
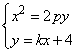 ,
,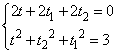 ,∴
,∴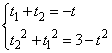 ,
,
 内的最大值为
内的最大值为 ,存在
,存在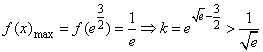 ,舍去;当
,舍去;当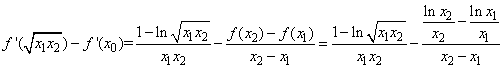 =
=
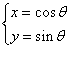 (θ为参数),消去参数θ,可得曲线C:x
(θ为参数),消去参数θ,可得曲线C:x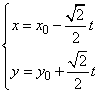 ,
,