字号： 默认 大 中 小
第Ⅰ卷 选择题
一、选择题。(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)
1、已知集合A＝{x∈N |x<8}，则下列关系式错误的是（ ）
A．0∈A B．1.5
A
C．－1
2、函数
的定义域是（ ）
A．(－1，0) ∪ (0，＋∞)
B．[－3，＋∞)
C．[－3，－1) ∪ (－1，＋∞)
D．(－1，＋∞)
3、设集合U＝R，集合A＝{x|x2－2x>0}，则
等于（ ）
A．{x |x<0或x>2) B．{x | x≤0或x≥2}
C．{x | 0≤x≤2) D．{x|0<x<2}
4、函数y＝ax在[0，1]上的最大值与最小值的和为3，则实数a等于（ ）
A．
B．2
C．4 D．
5、已知0<a<l，b<－1，则函数y＝ax＋b的图象必定不经过（ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
6、设函数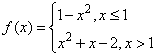
，则
的值为（ ）
A．
B．
C．
D．18
7、为了求函数f(x)＝2x＋3x－7的一个零点，某同学利用计算器得到自变量x和函数f(x)的部分对应值(精确度0.1)如下表所示：
x |
1.25 |
l.3125 |
1.375 |
1.4375 |
1.5 |
1.5625 |
f(x) |
－0.8716 |
－0.5788 |
－0.2813 |
0.210l |
0.32843 |
0.64115 |
则方程2x＋3x＝7的近似解(精确到0.1)可取为（ ）
A．1.32 B．1.39
C．1.4 D．1.3
8、对于函数f(x)＝ax3＋bx＋c(其中a，b，c∈Z)，选取a，b，c的一组值计算f(1)和f(－1)，所得出的正确结果一定不可能是（ ）
A．4和6 B．3和1
C．2和4 D．1和2
9、已知函数y＝f(1－x)的图象如图所示，则y＝f(1＋x)的图象为（ ）
10、对于任意实数x，符号[x]表示x的整数部分，即[x]是不超过x的最大整数，例如[2]＝2；[2.1]＝2；[－2.2]＝－3．即函数y＝[x]叫做“取整函数”，它在数学本身和生产实践中有广泛的应用，那么[log31]＋[log32]＋[log33]＋…＋[10g326]的值为（ ）
A．38 B．40
C．42 D．44
11、幂函数y＝xα，当α取不同的正数时，在区间[0，l]上它们的图象是一组美丽的曲线(如图)．设点A(1，0)，B(0，1)，连接AB，线段AB恰好被其中的两个幂函数y＝xα，y＝xβ的图象三等分，即有BM＝MN＝NA．那么αβ＝（ ）
A．1 B．2
C．3 D．无法确定
12、存在函数f(x)满足，对任意x∈R都有（ ）
A．f(x2)＝x B．f(x2＋x)＝x＋3
C．f(|log2x|)＝x2＋x D．f(x2＋2x)＝|x＋1|
第Ⅱ卷 非选择题
二、填空题(本大题共4小题，每小题5分，共20分)
13、函数y＝ax－2－1(a>0且a≠1)的图象必经过点_______．
14、集合A＝{3，log2a}，B＝{a，b}，若A∩B＝{2}，则A∪B＝______．
15、设f(x)是定义在R上的奇函数，且 y＝f(x)的图象关于直线
对称，则f(1)＋f(2)＋f(3)＋f(4)＋f(5)＝_______．
16、己知函数f(x)＝|log2x|，正实数m，n满足m<n，且f(m)＝f(n)，若f(x)在区间[m2，n]上的最大值为2，则m＋n＝______．
显示答案与解析
，则n＝2，∴
．三、解答题(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤)
；
．
．
，{1}，{2}，{1，2}；……5分
，此时
或
，不符合题意；19、(本题满分12分)设函数f(x)＝ax2＋bx＋l(a，b∈R)．
（1）若f(－1)＝0，且对任意实数x均有f(x)≥0，求实数a，b的值；
（2）在（1）的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围．
显示答案与解析
，
或
，20、(本题满分12分)某企业在2015年年底共有职工2000人，本年企业利润为3000万，从2016年起计划每年利润增加100万元，职工每年净增a人，设从2016年起的第x年(2016年为第一年)该企业人均利润为y万元．
（1）写出y与x之间的函数关系式；
（2）今后为使企业人均利润每年都是增长，那么该企业每年人口的净增不能超过多少人?
显示答案与解析
．…………5分
．
．
，
，∴
．∵a∈N21、(本题满分12分)已知函数f(x)满足
，其中a>0，且a≠1．
（1）对于函数f(x)，当x∈(－1，1)时，f(1－m)＋f(1－m2)<0，求实数m值的集合；
（2）当x∈(－∞，2)时，
的值恒为负数，求a的取值范围．
，即
（x∈R）．
；…… 8分
也是增函数，
在指定区间上恒为负数，
，即
，
．…… 12分22、(本题满分12分)函数
，g(x)＝1＋loga(x－1)(a>0，且a≠1)，设f(x)和g(x)定义域的公共部分为D．
（1）求集合D；
（2）当a>1时，若不等式
在D内恒成立，求a的取值范围；
（3）是否存在实数a，使得
时，f(x)在[m，n]上的值域是[g(n)，g(m)]．若存在求a的取值范围；若不存在说明理由．