字号: 默认 大 中 小
第Ⅰ卷 选择题
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.经过圆![]() 的圆心且与直线
的圆心且与直线![]() 平行的直线方程是( )
平行的直线方程是( )
A、
B、
C、
D、
2.已知直线![]() ,
,![]() ,若
,若![]() ,则m的值是( )
,则m的值是( )
A、
B、-2
C、
D、2
3.某几何体的三视图如图所示,当a+b取最大值时,该几何体体积为( )
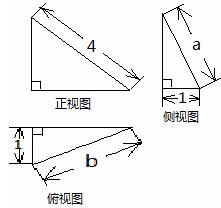
A、
B、
C、
D、
4.如图正方体ABCD—A1B1C1D1的棱长为2,线段B1D1上有两个动点E、F,且EF=1则下列结论中错误的是( )

A、EF∥平面ABCD B、AC⊥BE
C、三棱锥A—BEF体积为定值 D、ΔBEF与ΔAEF面积相等
5.已知{an}是等差数列,a3=8,S6=57,则过点P(2,a7),Q(3,a8)的直线斜率为( )
A、3 B、
C、—3 D、—13
6.若点(1,1)和点(0,2)一个在圆![]() 的内部,另一个在圆的外部,则正实数a的取值范围是( )
的内部,另一个在圆的外部,则正实数a的取值范围是( )
A、
B、
C、(0,1) D、(1,2)
7.如图,在四面体A—BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设![]() ,则( )
,则( )
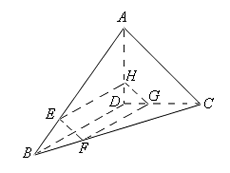
A、函数f(x)的值域为(0,1]
B、函数y=f(x)满足f(x)=f(2-x)
C、函数y=f(x)的最大值为2
D、函数y=f(x)在
上单调递增
8.正四面体ABCD的外接球半径为6,过棱AB作该球的截面,则截面面积的最小值为( )
A、9π B、4π
C、24π D、16π
9.已知圆![]() 与圆
与圆![]() 关于直线
关于直线![]() 对称,则直线
对称,则直线![]() 的方程可以是( )
的方程可以是( )
A、x-y+1=0 B、x-y-2=0
C、3x-2y+1=0 D、x+y-1=0
10.在正方体ABCD—A1B1C1D1中,直线BC1与平面A1BD所成角的余弦值为( )
A、
B、
C、
D、
11.如果直线![]() 和函数
和函数![]() 的图像恒过同一个定点,且该定点始终落在圆
的图像恒过同一个定点,且该定点始终落在圆![]() 的内部或圆上,那么,
的内部或圆上,那么,![]() 的取值范围是( )
的取值范围是( )
A、
B、
C、
D、
12.圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
A、
B、
C、
D、
第Ⅱ卷 非选择题
二、填空题(本大题共四小题,每小题5分,共20分)
13.在底面直径为4的圆柱形容器中,放入一个半径为1的冰球,当冰球全部融化后,容器中液面的高度为___________(相同体积的冰与水的质量比为9:10)
14.已知三个不同的平面α、β、γ和两条不同的直线m、n,有下列五个命题:
①若m∥n,m⊥α,则n⊥α;②若m⊥α,m⊥β,则α∥β
③若m⊥α,m∥n,![]() ,则α⊥β④若
,则α⊥β④若![]() 则m∥n
则m∥n
⑤若![]() 且
且![]() 则
则![]()
其中正确命题的编号是______________.
15.在ΔABC中,角A、B、C的对边分别为a、b、c,若![]() ,则直线ax+by-c=0被圆x2+y2=4所截得的弦长为__________.
,则直线ax+by-c=0被圆x2+y2=4所截得的弦长为__________.
16.设P(4,0),A、B是圆C:x2+y2=4上关于x轴对称的任意两个不同的点,连接PB交圆C于另一点E,直线AE与x轴交于点T,则|AT|×|TE|=___________.
显示答案与解析三、解答题(解答应写出文字说明,证明过程或者演算步骤)
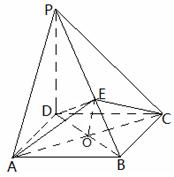
17.(10分)如图所示,在四棱锥P—ABCD中,PD⊥平面ABCD,底面ABCD是菱形,![]() ,AB=2,
,AB=2,![]() ,O为AC与BD的交点,E为棱PB上一点.
,O为AC与BD的交点,E为棱PB上一点.
(1)证明:平面EAC⊥平面PBD;
(2)若三棱锥P—EAD的体积为![]() ,求证:PD∥平面EAC.
,求证:PD∥平面EAC.
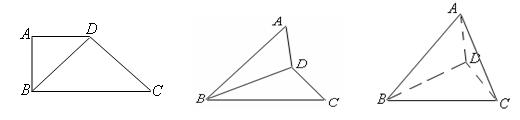
18.(12分)在梯形ABCD中,AD∥BC,BC=2AD,![]() ,AB⊥BC,如图把ΔABD沿BD翻折,使得平面ABD⊥平面BCD,
,AB⊥BC,如图把ΔABD沿BD翻折,使得平面ABD⊥平面BCD,
(1)求证:CD⊥平面ABD;
(2)若M为线段BC的中点,求点M到平面ACD的距离.
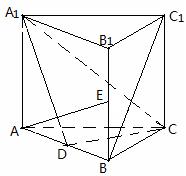
19.(12分)如图,直三棱柱ABC—A1B1C1中,D、E分别是AB、BB1的中点,![]() ,AA1=AC=CB=1.
,AA1=AC=CB=1.
(1)求异面直线AE与BC1所成角的余弦值;
(2)求二面角D—A1C—A的正切值
20.(12分)已知数列{an}(n=1,2,3,……),⊙C1:![]() 和⊙C2:
和⊙C2:![]() ,若⊙C1与⊙C2交于A、B两点,且这两点平分圆C2的周长.
,若⊙C1与⊙C2交于A、B两点,且这两点平分圆C2的周长.
(1)求证数列{an}是等差数列;
(2)若a1=1,则当⊙C1面积最小时,求出⊙C1的方程.
显示答案与解析22.(12分)已知圆C过点![]() 且与圆M:
且与圆M:![]() 关于直线x+y+4=0对称,定点R的坐标为(1,1).
关于直线x+y+4=0对称,定点R的坐标为(1,1).
(1)求圆C的方程;
(2)设Q为圆C上的一个动点,求![]() 的最小值;
的最小值;
(3)过点R作两条相异直线分别与圆C相交于A、B,且直线RA和直线RB的倾斜角互补,O为坐标原点,试判断直线OR和直线AB是否平行,并说明理由.
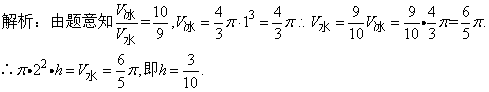
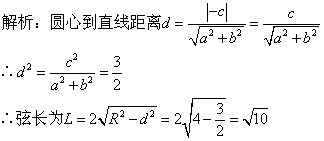

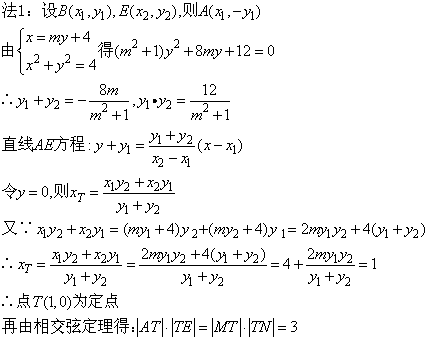

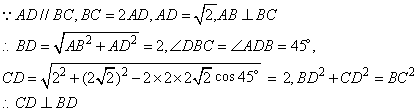
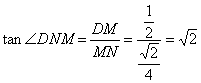 ……12分
……12分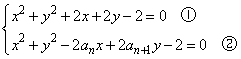 ……1分
……1分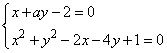
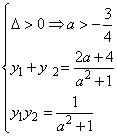 ①……7分
①……7分