字号： 默认 大 中 小
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知集合A={x|x2－2x－3≤0}，B={x|y=ln（2－x）}，则A∩B=（ ）
A．（1，3） B．（1，3]
C．[－1，2） D．（－1，2）
2．若复数
是纯虚数（i为虚数单位），则
的值为（ ）
A．－7 B．
C．7 D．－7或
3．在各项均为正数的等比数列{an}中，a1=2，且a2，a4＋2，a5成等差数列，记Sn为数列{an}的前n项和，则S5=（ ）
A．32 B．62
C．27 D．81
4．已知函数
的最小正周期为π，且其图像向左平移
个单位后得到函数
的图像，则函数f（x）的图像（ ）
A．关于直线
对称 B．关于直线
对称
C．关于点
对称 D．关于点
对称
5．甲、乙、丙、丁、戊五位同学站成一排照相留念，则在甲乙相邻的条件下，甲丙也相邻的概率为（ ）
A．
B．
C．
D．
6．已知定义在R上的函数f（x）满足
，
，且当
时，
，则f（31）=（ ）
A．0 B．1
C．－1 D．2
7．若如下框图所给的程序运行结果为s=41，则图中的判断框①中应填入的是（ ）
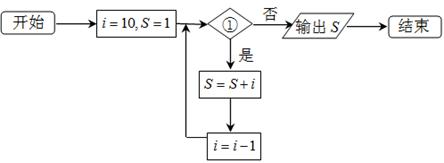
A．i＞6？ B．i≤6？
C．i＞5？ D．i＜5？
8．有6名选手参加演讲比赛，观众甲猜测：4号或5号选手得第一名；观众乙猜测：3号选手不可能得第一名；观众丙猜测：1，2，6号选手中的一位获得第一名；观众丁猜测：4，5，6号选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1人猜对比赛结果，此人是（ ）
A．甲 B．乙
C．丙 D．丁
9．设F1，F2为椭圆
的两个焦点，点P在椭圆上，若线段PF1的中点在y轴上，则
的值为（ ）
A．
B．
C．
D．
10．已知变量x，y满足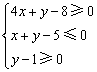
，若目标函数
取到最大值6，则a的值为（ ）
A．2 B．
C．
D．－2
11．如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为（ ）
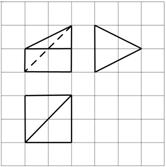
A．8π B．
C．12π D．
12．已知直线
与曲线
相交，且曲线C在交点A，B处的切线平行，则实数p的值为（ ）
A．4 B．4或－3
C．－3或－1 D．－3
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题5分，共20分．
13．已知
，则二项式
的展开式中
的系数为__________．
14．在Rt△ABC中，∠A=90°，AB=AC=2，点D为AC中点，点E满足
，则
=__________．
15．已知双曲线
的渐近线被圆
截得的弦长为2，则该双曲线的离心率为__________．
16．已知数列{an}的前n项和为Sn，对任意
，
且
恒成立，则实数t的取值范围是__________．
三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）在△ABC中，角A，B，C的对边分别为a，b，c，且满足
．
（Ⅰ）求角B的大小；
（Ⅱ）若点M为BC中点，且AM=AC，求sin∠BAC．
18．（本小题满分12分）某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查，如下表：（平均每天锻炼的时间单位：分钟）
平均每天锻炼 的时间（分钟） |
[0，10） |
[10，20） |
[20，30） |
[30，40） |
[40，50） |
[50，60） |
总人数 |
20 |
36 |
44 |
50 |
40 |
10 |
将学生日均课外体育运动时间在[40，60）上的学生评价为“课外体育达标”．
（Ⅰ）请根据上述表格中的统计数据填写下面2×2列联表，并通过计算判断是否能在犯错误的概率不超过
的前提下认为“课外体育达标”与性别有关？
|
课外体育不达标 |
课外体育达标 |
合计 |
男 |
|
|
|
女 |
|
20 |
110 |
合计 |
|
|
|
（Ⅱ）将上述调查所得到的频率视为概率．现在从该校高三学生中，抽取3名学生，记被抽取的3名学生中的“课外体育达标”学生人数为X，若每次抽取的结果是相互独立的，求X的数学期望和方差．
参考公式：
，其中
．
参考数据：
P（K2≥k0） |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
k0 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
19．（本小题满分12分）已知四棱锥P—ABCD，底面ABCD是直角梯形，AD∥BC，∠BCD=90°，
，△ABM是边长为2的等边三角形，
．
（Ⅰ）求证：平面
；
（Ⅱ）若点E为PC中点，求二面角P—MD—E的余弦值．
20．（本题满分12分）已知抛物线x2=2py上点P处的切线方程为x－y－1=0．
（Ⅰ）求抛物线的方程；
（Ⅱ）设A（x1，y1）和B（x2，y2）为抛物线上的两个动点，其中y1≠y2且y1＋y2=4，线段AB的垂直平分线l与y轴交于点C，求△ABC面积的最大值.
21．（本题满分12分）已知函数
．
（Ⅰ）当
时，求f（x）的单调性；
（Ⅱ）若
，且方程h（x）=m有两个不相等的实数根x1，x2．求证：x1＋x2＞1．
22．（本小题满分10分）选修4－1 ：几何证明选讲
如图，在锐角三角形ABC中，AB=AC，以AB为直径的圆O与边BC，AC另外的交点分别为D，E，且DF⊥AC于F．
（Ⅰ）求证：DF是⊙O的切线；
（Ⅱ）若CD=3，
，求AB的长．
23．（本小题满分10分）选修4－4：坐标系与参数方程
以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，已知点P的直角坐标为（1，2），点M的极坐标为
，若直线l过点P，且倾斜角为
，圆C以M为圆心，3为半径．
（Ⅰ）求直线l的参数方程和圆C的极坐标方程；
（Ⅱ）设直线l与圆C相交于A，B两点，求|PA|·|PB|．
24．（本小题满分10分）选修4－5：不等式选讲
已知函数
的定义域为R．
（Ⅰ）求实数m的范围；
（Ⅱ）若m的最大值为n，当正数a，b满足
时，求4a＋7b的最小值．