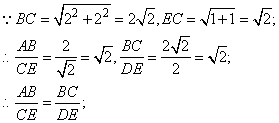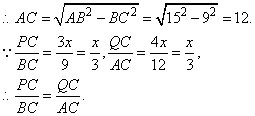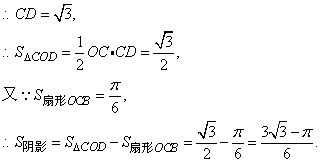字号： 默认 大 中 小
时间：120分钟 满分：120分
一、选择题（共7小题，每小题3分，满分21分）
1、中国的海洋面积约为370000km2，将数370000用科学记数法表示为（ ）
A．37×104 B．3.7×104
C．0.37×106 D．3.7×105
2、下列事件是不可能事件的是（ ）
A．射击运动员只射击1次，就命中靶心
B．任取一个实数x，都有|x|≥0
C．画一个三角形，使其三边的长分别为8cm，6cm，2cm
D．抛一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子，朝上一面的点数为6
3、甲乙两人同时从A地出发到B地，如果甲的速度v保持不变，而乙先用
的速度到达中点，再用2v的速度到达B地，则下列结论中正确的是（ ）
A．甲乙同时到达B地
B．甲先到达B地
C．乙先到达B地
D．谁先到达B地与速度v有关
4. 在长方形ABCD中AB＝16，如图所示裁出一扇形ABE，将扇形围成一个圆锥（AB和AE重合），则此圆锥的底面半径为（ ）
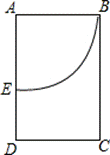
A．4 B．16
C．
D．8
5、如图，在等腰△ABC中，AB＝AC，BD⊥AC，∠ABC＝72°，则∠ABD＝（ ）
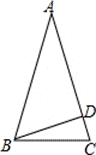
A．36° B．54°
C．18° D．64°
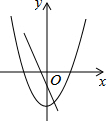
6、在同一坐标系中，一次函数y＝ax＋2与二次函数y＝x2＋a的图象可能是（ ）
A．
B．
C．
D．
7、已知m＝x＋1，n＝－x＋2，若规定
，则y的最小值为（ ）
A．0 B．1
C．－1 D．2
第Ⅱ卷 非选择题
二、填空题（共7小题，每小题3分，满分21分）
8、若二次根式
有意义，则x的取值范围是__________．
9、因式分解：x2－49＝__________．
10、关于x的一元二次方程2x2－4x＋m－1＝0有两个不相等的实数根，则m的取值范围为__________．
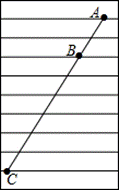
11、如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点A、B、C都在横格线上．若线段AB＝4cm，则线段BC＝__________cm．
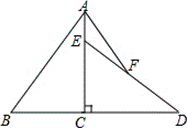
12、如图，已知Rt△ABC中，∠ACB＝90°，AC＝12，BC＝8，将△ABC绕直角顶点C顺时针旋转90°得到△DEC．若点F是DE的中点，连接AF，则AF＝__________．
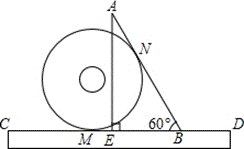
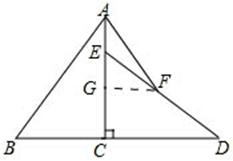
13、小明把半径为
的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上，此时，光盘与AB，CD分别相切于点N，M．现从如图所示的位置开始，将光盘在直尺边上沿着CD向右滚动到再次与AB相切时，光盘的圆心经过的距离是__________．
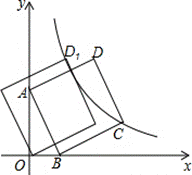
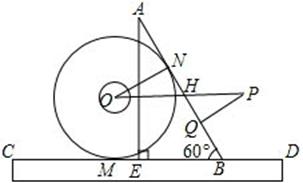
14、如图，直线y＝－3x＋6与x轴交于点B，与y轴交于点A，以线段AB为边，在第一象限内作正方形ABCD，点C落在双曲线
上，将正方形ABCD沿x轴负方向平移a个单位长度，使点D恰好落在双曲线
上的点D1处，则a＝__________.
．
，
．
上的点D三、解答题（共10小题，满分78分）
．
16、（本题满分6分）如图，△ABC和△DEC的顶点都在边长为1的小正方形的顶点上．
（1）填空：∠ABC＝__________，BC＝__________；
（2）判断△ABC与△DEC是否相似，并证明你的结论．
；
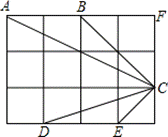
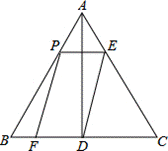
17、（本题满分6分）如图，在等边△ABC中，AB＝6，AD⊥BC于点D．点P在边AB上运动，过点P作PE∥BC，与边AC交于点E，连接ED，以PE、ED为邻边作平行四边形
PEDF．设线段AP的长为x（0＜x＜6）．
（1）求线段PE的长．（用含x的代数式表示）
（2）当四边形PEDF为菱形时，求x的值．
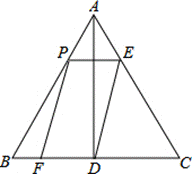
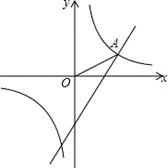
18、（本题满分6分）如图，在同一直角坐标系中，一次函数
的图象和反比例函数
的图象的一个交点为
．
（1）求m的值及反比例函数的解析式．
（2）若点P在x轴上，且△AOP为等腰三角形，请直接写出点P的坐标（写出两个即可）．
的图象经过点
，
，
，
的图象经过点A，
，
；
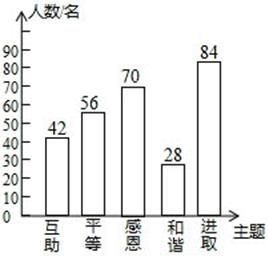
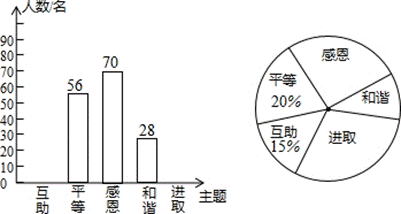
19、（本题满分6分）某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：
（1）这次调查的学生共有多少名？
（2）请将条形统计图补充完整，并在扇形统计图中标出“进取”所对应的圆心角的度数．
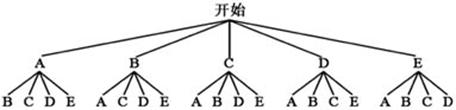
（3）如果要在这5个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．
．20、（本题满分6分）某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求，商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．
（1）该商家购进的第一批衬衫是多少件？
（2）若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完后利润率不低于25%（不考虑其他因素），那么每件衬衫的标价至少是多少元？
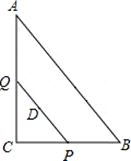
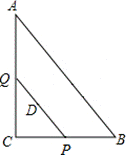
，21、（本题满分8分）如图，Rt△ABC中，∠C＝90°，AB＝15，BC＝9，点P，Q分别在BC，AC上，CP＝3x，CQ＝4x（0＜x＜3）．点D在线段PQ上，且PD＝PC．
（1）求证：PQ∥AB；
（2）若点D在∠BAC的平分线上，求CP的长．
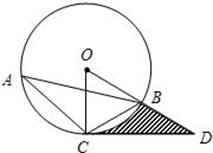
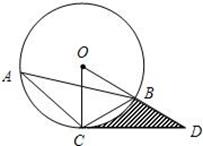
22、（本题满分8分）如图，△ABC内接于⊙O，点D在半径OB的延长线上，∠BCD＝∠A＝30°．
（1）试判断直线CD与⊙O的位置关系，并说明理由；
（2）若⊙O的半径长为1，求由弧BC、线段CD和BD所围成的阴影部分面积．
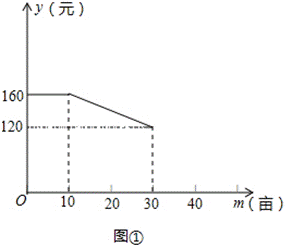
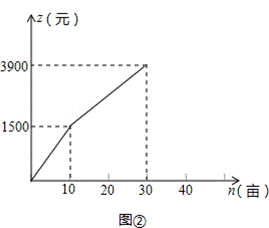
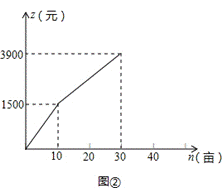
23、（本题满分12分）某农庄计划在30亩空地上全部种植蔬菜和水果，菜农小张和果农小李分别承包了种植蔬菜和水果的任务，小张种植每亩蔬菜的工资y（元）与种植面积m（亩）之间的函数关系如图①所示，小李种植水果所得报酬z（元）与种植面积n（亩）之间的函数关系如图②所示．
（1）如果种植蔬菜20亩，则小张种植每亩蔬菜的工资是__________元，小张应得的工资总额是__________元，此时，小李种植水果__________亩，小李应得的报酬是__________元；
（2）请直接写出y与m，z与n之间的函数关系式．
（3）设农庄支付给小张和小李的总费用为W（元），求W与m之间的函数关系式，并求出总费用最大为多少？
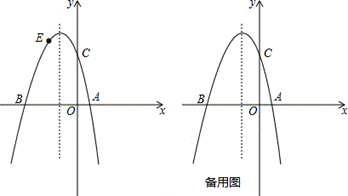
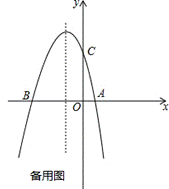
24、（本题满分14分）如图，已知抛物线y＝ax2＋bx＋c（a≠0）与x轴交于点A（1，0）和点B（－3，0），与y轴交于点C，且OC＝OB．
（1）求此抛物线的解析式；
（2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；
（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．
（4）连接AC，H是抛物线上一动点，过点H作AC的平行线交x轴于点F．是否存在这样的点F，使得以A，C，H，F为顶点所组成的四边形是平行四边形？若存在，求出满足条件的点F的坐标；若不存在，请说明理由．
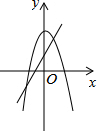
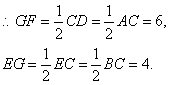
