字号: 默认 大 中 小
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,总分150分,考试时间120分钟.
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)
1、已知A={y|y=log2x,x>1},![]() ,则A∩B=( )
,则A∩B=( )
A.
B.(0,1)
C.
D.
2、下表是某厂1—4月份用水量(单位:百吨)的一组数据:
月份x |
1 |
2 |
3 |
4 |
用水量y |
4.5 |
4 |
3 |
2.5 |
由散点图可知,用水量与月份之间有较好的线性相关关系,其线性回归方程为y=-0.7x+a,则a等于( )
A.10.5 B.5.15
C.5.2 D.5.25
3、若在![]() 的展开式中含有常数项,则正整数n取得最小值时的常数项为( )
的展开式中含有常数项,则正整数n取得最小值时的常数项为( )
A.
B.-135
C.
D.135
4、若f′(x0)=2,则![]() 等于( )
等于( )
A.-1 B.-2
C.1 D.
5、已知随机变量X服从正态分布N(2,σ2),其正态分布密度曲线为函数f(x)的图象,且![]() 则P(x>4)=( )
则P(x>4)=( )
A.
B.
C.
D.
6、设点A是曲线![]() 上的任意一点,P点处的切线的倾斜角为α,则角α的取值范围是( )
上的任意一点,P点处的切线的倾斜角为α,则角α的取值范围是( )
A.
B.
C.
D.
7、已知![]() ,则f(k+1)-f(k)等于( )
,则f(k+1)-f(k)等于( )
A.
B.
C.
D.
8、若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”,现从1,2,3,4,5,6这六个数字中任取3个数,组成无重复数字的三位数,其中“伞数”有( )
A.120个 B.80个
C.40个 D.20个
9、下列判断错误的是( )
A.若随机变量ξ服从正态分布N(1,σ2),P(ξ≤4)=0.79,则P(ξ≤-2)=0.21
B.若n组数据(x1,y1)…(xn,yn)的散点都在y=-2x+1上,则相关系数r=-1
C.若随机变量ξ服从二项分布:
,则Eξ=1
D.“am2<bm2”是“a<b”的必要不充分条件
10、为大力提倡“厉行节约,反对浪费”,我市通过随机询问100名性别不同的居民是否做到“光盘”行动,得到如下列联表及附表:经计算:![]() ,参照附表,得到的正确结论是( )
,参照附表,得到的正确结论是( )
|
做不到“光盘”行动 |
做到“光盘”行动 |
男 |
45 |
10 |
女 |
30 |
15 |
P(K2≥k) |
0.10 |
0.05 |
0.025 |
k |
2.706 |
3.841 |
5.024 |
A.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别无关”
C.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别有关”
D.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别无关”
11、给出下列四个命题:
①f(x)=x3-3x2是增函数,无极值.
②f(x)=x3-3x2在(-∞,2)上没有最大值
③由曲线y=x,y=x2所围成图形的面积是
④函数f(x)=lnx+ax存在与直线2x-y=0平行的切线,则实数a取值范围是(-∞,2).
其中正确命题的个数为( )
A.1 B.2
C.3 D.4
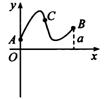
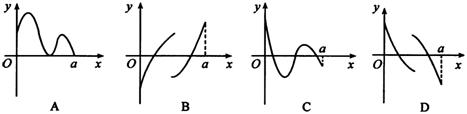
12、定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为s(x),则函数s(x)的导函数s′(x)的图象大致是( )
二、填空题(每小题5分,共20分)
13、下面是关于复数![]() 的四个命题:p1:|z|=2,p2:z2=2i,p3:z的共轭复数为1+i,p4:z的虚部为-1,其中真命题的个数为__________.
的四个命题:p1:|z|=2,p2:z2=2i,p3:z的共轭复数为1+i,p4:z的虚部为-1,其中真命题的个数为__________.
14、某校开设九门课程供学生选修,其中A,B,C三门由于上课时间相同,至多选一门,若学校规定每位学生选修四门,则不同的选修方案共有__________种.
15、二维空间中,圆的一维测度(周长)l=2πr;二维测度(面积)S=πr2;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)![]() ,应用合情推理,若四维空间中,“超球”的三维测度V=8πr3,则其四维测度W=__________.
,应用合情推理,若四维空间中,“超球”的三维测度V=8πr3,则其四维测度W=__________.
16、已知![]() ,x∈R,若至少存在一个实数x使得f(a-x)+f(ax2-1)<0成立,a的范围为__________.
,x∈R,若至少存在一个实数x使得f(a-x)+f(ax2-1)<0成立,a的范围为__________.
三、解答题(本大题共6小题,70分)
17、(本题满分12分)已知:全集U=R,函数![]() 的定义域为集合A,集合B={x|x2-a<0}.
的定义域为集合A,集合B={x|x2-a<0}.
(1)求
;
(2)若A∪B=A,求实数a的范围.
18、(本题满分12分)已知函数![]() (a,b为常数),且
(a,b为常数),且![]() ,且f(0)=0.
,且f(0)=0.
(I)求函数f(x)的解析式;
(Ⅱ)判断函数f(x)在定义域上的奇偶性,并证明;
(Ⅲ)对于任意的x∈[0,2],f(x)(2x+1)<m·4x恒成立,求实数m的取值范围.
19、(本题满分12分)甲、乙两位小学生各有2008年奥运吉祥物“福娃”5个(其中“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮”各一个),现以投掷一个骰子的方式进行游戏,规则如下:当出现向上的点数是奇数时,甲赢得乙一个福娃;否则乙赢得甲一个福娃,规定掷骰子的次数达9次时,或在此前某人已赢得所有福娃时游戏终止.记游戏终止时投掷骰子的次数为ξ.
(1)求掷骰子的次数为7的概率;
(2)求ξ的分布列及数学期望Eξ.
20、(本小题满分12分)一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元.设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4-x万元,且每万件国家给予补助![]() 万元.(e为自然对数的底数,e是一个常数.)
万元.(e为自然对数的底数,e是一个常数.)
(I)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式;
(Ⅱ)当月生产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生产量(万件).(注:月利润=月销售收入+月国家补助-月总成本).
四、选考题(本题满分10分)(请在以下甲、乙、丙三个选考题中任选一个作答,多答则以第一个计分)
23、选修4—4:坐标系与参数方程
已知曲线C的参数方程是![]() ,直线l的参数方程为
,直线l的参数方程为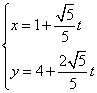 (t为参数),
(t为参数),
(1)求曲线C与直线l的普通方程;
(2)若直线l与曲线C相交于P,Q两点,且![]() ,求实数m的值.
,求实数m的值.
24、选修4—5:不等式选讲
设函数f(x)=|x-1|+|x-a|.
(1)若a=-1,解不等式f(x)≥3;
(2)如果
R,f(x)≥2,求a的取值范围.
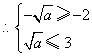 .
. ,可得:
,可得: